Algorithmus (2D-FFT-Filter)
2D-FFT-Filter werden verwendet, um 2D-Signale zu verarbeiten, einschließlich Matrix und Bild. Zuerst wird eine zweidimensionale schnelle Fourier-Transformation (2D-FFT) durchgeführt, dann wird ein Frequenzdomainfilter angewendet und schließlich wird eine 2D-IFFT durchgeführt, um das gefilterte Ergebnis zurück in die räumliche Domain zu konvertieren.
Fünf Filtertypen und vier Fensterarten sind für die 2D-FFT-Filter verfügbar.
Filtertypen
Die Filtertypen schließen Tiefpass, Hochpass, Bandpass, Bandblock und Schwellenwert mit ein.
Beachten Sie, dass Hochpass, Bandpass und Bandblock alle mit Hilfe des Tiefpass' erstellt werden können.
Die Filtertypen der 2D FFT-Filter werden in der folgenden Tabelle aufgeführt. Um die 2D-Filtertypen von Tiefpass, Hochpass, Bandpass und Bandblock einfacher zu verstehen, wird für jeden Filtertyp das ideale Fenster in der Tabelle verwendet.
Für einen 2D-Filter H(u,v), u=0, 1,.., M-1, v=0, 1,..., N-1. Normieren Sie die Frequenzkoordinaten: m=(u-M/2)/M, n=(v-N/2)/N, where -0,5<m<0,5 -0,5<n<0,5 . r ist definiert als:
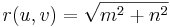 und und 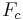 sind die Grenzfrequenz. sind die Grenzfrequenz.
| Tiefpass |
Blockiert die Frequenzkomponenten über der Grenzfrequenz und lässt nur die niedrigen Frequenzkomponenten durch.
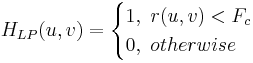
|
| Hochpass |
Blockt die Frequenzkomponenten, die unter der Grenzfrequenz liegen.
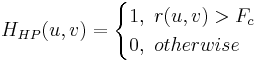
Beachten Sie, dass 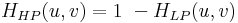 . .
|
| Bandpass |
Lässt die Frequenzen innerhalb eines bestimmten Bereichs, der durch die untere und obere Grenzfreqzenz definiert wird, durch.
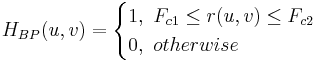
Beachten Sie, dass 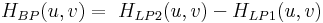 . .
wobei 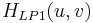 und und 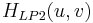 Tiefpassfilter sind mit der jeweils unteren und oberen Frequenz Fc1 und Fc2. Tiefpassfilter sind mit der jeweils unteren und oberen Frequenz Fc1 und Fc2.
|
| Bandblock |
Entfernt die Frequenzen innerhalb des gewählten Bereichs.
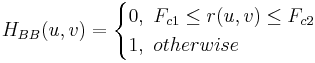
Beachten Sie, dass 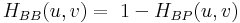 . .
|
| Schwellenwert |
Lässt nur Frequenzkomponenten durch, deren Amplituden zwischen dem unteren Schwellenwert und dem oberen Schwellenwert liegen.
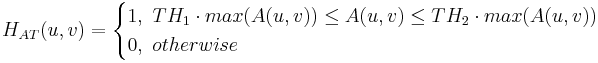
Wobei 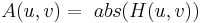 , , 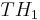 und und 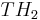 die unteren und oberen Schwellenwerte sind. die unteren und oberen Schwellenwerte sind.
Beachten Sie, dass das Fenster nicht für den Filtertyp Schwellenwert verwendet wird.
|
Fenstertypen
Fenstertypen der 2D FFT-Filter schließen Butterworth, Ideal, Gaussian und Blackman ein.
Hochpass-, Bandpass- und Bandblockfilter können alle aus dem Tiefpassfilter für andere Fenstertypen auf die gleiche Weise erstellt werden wie das Idealfenster, das in der Tabelle der Filtertypen aufgelistet wird. Daher werden nur Tiefpassfilter für jeden Fenstertyp folgendermaßen eingeführt.
Eine gängige Möglichkeit, einen 2D-Filter zu erzeugen, besteht darin, das entsprechende 1D-Filterfenster im m - n normierten Frequenzbereich zu drehen, d.h., verwenden Sie 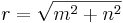 , um die Variable im Fenster der 1D-Butterworth-Funktion zu ersetzen. Die Erzeugung des 2D-Butterworth-Tiefpassfilters dient als Beispiel, um die Vorgehensweise zu beschreiben. , um die Variable im Fenster der 1D-Butterworth-Funktion zu ersetzen. Die Erzeugung des 2D-Butterworth-Tiefpassfilters dient als Beispiel, um die Vorgehensweise zu beschreiben.
Butterworth
Die Fensterfunktion 1D Butterworth wird ausgedrückt mit:
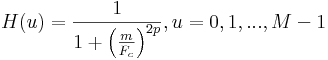
Parameter werden folgendermaßen beschrieben:
- m = (u - M/2) / M : die normierte Frequenz im Bereich [-0,5, 0,5], +/- 0,5 entspricht der halben Nyquist-Frequenz Beachten Sie, dass die anderen Normierungsmethoden auch gefunden werden können. Diese wird in diesem Fall ausgewählt, weil der Peak des Filters an der DC-Komponente des FFT-Ergebnisses ausgerichtet sein muss.
- Fc: die Grenzfrequenz, die sich im Bereich (0, 0,5] befindet. Die Grenzfrequenz ist ein Schlüsselparameter für einen Filter. Für Butterworth ist die Grenzfrequenz die Frequenz, bei der sich H(u) auf das 0,5-fache seines maximalen Werts verringert. Je größer Fc ist, desto glatter ist der Filter. Im Allgemeinen eignet sich ein glatterer Filter besser zum Reduzieren des negativen Ringeffekts, der von der FFT-Filterung verursacht wird.
- p: die Filterordnung, eine ganze Zahl Je kleiner p ist, desto glatter ist der Filter.
Für eine 2D-FFT-Filter sei m = ( u - M/2 ) / M, n = (v - N/2 ) / N. Beides, m und n, liegen im Bereich [-0,5, 0,5]. Drehen Sie das 1D-Butterworth-Fenster in dem m - n normierten Frequenzbereich und lassen Sie 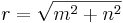 . Der 2D-Butterworth-Tiefpassfilter kann ausgedrückt werden als: . Der 2D-Butterworth-Tiefpassfilter kann ausgedrückt werden als:
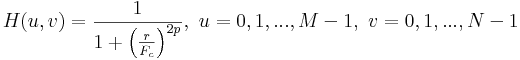
H(u,v) sollte nur Werte in einem kreisförmigen Bereich nehmen, dessen Radius bestimmt wird durch R = max(-m[0], m[M-1], -n[0], n[N-1] ). Wenn r > R ist, sollte der Wert von H(u,v) auf Null gesetzt werden. Die Grenzfrequenz Fc liegt in dem Bereich (0, R].
Die Grenzfrequenz wird normiert durch 2R, so dass der Wertebereich von Fc immer (0, 0,5] ist.
Die Vorgehensweise zum Erstellen eines 2D-FFT-Filters wird im Folgenden gezeigt.
/Algorithm_make_2d_filter.png)
Ein 2D-Butterworth-Tiefpassfilter für Fc=0,3, p=1 sieht folgendermaßen aus.
/Algorithm_bw_filter.png)
Ideal
Der Ideal-Filter wird in der Tabelle der Filtertypen eingeführt.
Gaussian
Der Tiefpassfilter 2D-Gaussian kann ausgedrückt werden als:
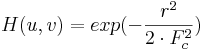
Die Grenzfrequenz für einen 2D-Gaussian-Filter ist diejenige, bei der H(u,v) sich auf das 0,607-fache seines maximalen Werts verringert. Größere Werte von Fc entsprechen einem glatteren Filter.
Ein 2D-Gaussian-Tiefpassfilter für Fc=0,2 sieht folgendermaßen aus.
/Algorithm_gau_filter.png)
Blackman
Der Tiefpassfilter 2D-Blackman kann ausgedrückt werden als: 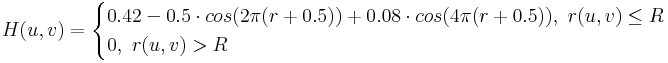
Beachten Sie, dass diese Fensterfunktion sich geringfügig von der bekannten Standardform unterscheidet, die Hochpass entspricht. Hier soll ein Tiefpassfilter verwendet werden, daher wird 0,5 zu r hinzugefügt, um den Filter in einen Tiefpass umzuwandeln.
2D-FFT-Filter in OriginPro bieten eine Option zum Fenster abschneiden, um zu entscheiden, ob das Blackman-Fenster abgeschnitten wird.
2D-Blackman-Tiefpassfilter ohne (erster Graph) und mit (zweiter Graph) Abschneiden werden jeweils im Folgenden gezeigt.
/Algorithm_bmn_filter.png) /Algorithm_bmw_filter.png)
Grenzwert
2D-FFT-Filter in OriginPro unterstützen vier Methode zum Festlegen des Grenzwerts. Dabei handelt es sich um Bruch, Fourier Pixel, Wellenlänge und Hertz. Die Verhältnisse dieser vier Methoden werden im Folgenden aufgelistet.
| Fourier Pixel |
Pixel in der Matrix, die die Daten speichert. Der Wert kann jede positive Zahl des Typs double sein. |
| Bruch |
Bruch = Fourier Pixel / sqrt( (cols/2)^2+(rows/2)^2 ), wobei cols und rows jeweils die Anzahl der Spalten und Zeilen darstellen. |
| Wellenlänge |
Wellenlänge = (cols-1) / Fourier Pixel |
| Hertz |
Hertz = Fourier Pixel / cols |
|