ExpGrow3Dec2

目次

関数

y=\left\{\begin{matrix} y_{0}+A_{d1}+A_{d2}+A_{g1}\left ( e^{-x_{c}/t_{g1}}-e^{-x/t_{g1}} \right )+A_{g2}\left ( e^{-x_{c}/t_{g2}}-e^{-x/t_{g2}} \right )+A_{g3}\left ( e^{-x_{c}/t_{g3}}-e^{-x/t_{g3}} \right ) \quad x\leq x_{c}\\ y_{0}+A_{d1}e^{-\left ( x-x_{c} \right )/t_{d1}}+A_{d2}e^{-\left ( x-x_{c} \right )/t_{d2}} \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad x>x_{c} \end{matrix}\right.

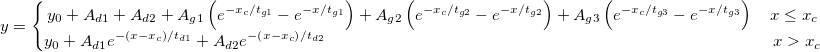
簡単な説明

3次増加と2次減少の位相の指数関数

サンプル曲線

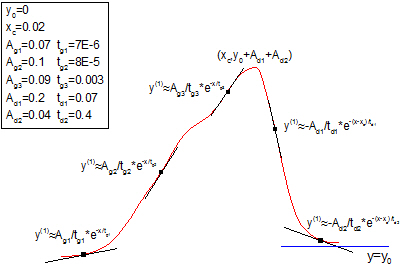
ExpGrow3Dec2.jpg

パラメータ

数：12

名前: y0, xc, Ag1, tg1, Ag2, tg2, Ag3, tg3, Ad1, td1, Ad2, td2

平均：y0 = オフセット, xc = 中心, Ag1,Ag2,Ag3 = 増加振幅, tg1,tg2 = 増加定数, Ad1,Ad2 = 減少振幅, td1,td2 = 減少定数

下側境界:0 < xc, Ag1, tg1, Ag2, tg2, Ag3, tg3, Ad1, td1, Ad2, td2

上側境界: なし

派生パラメータ

スクリプトでのアクセス法

nlf_ExpGrow3Dec2(x,y0,xc,Ag1,tg1,Ag2,tg2,Ag3,tg3,Ad1,td1,Ad2,td2)

関数定義ファイル名

fitfunc\ExpGrow3Dec2.fdf

カテゴリ

Exponential
English | Deutsch | 日本語