ExpDec3ExpDec3-FitFunc
関数
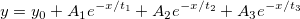
説明
一定時間パラメータの3次指数減少関数
サンプル曲線
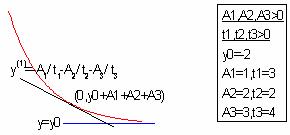
パラメータ
数: 7
パラメータの名前: y0, A1, t1, A2, t2, A3, t3
意味:y0 = オフセット, A1 = 振幅, t1 = 時間定数 (崩壊定数), A2 = 振幅, t2 = 時間定数 (崩壊定数)), A3 = 振幅, t3 = 時間定数 (崩壊定数)
下側境界: なし
上側境界: なし
Note: t1・t2・t3ではそれぞれ異なる初期パラメータが使用され、フィット結果として t3 > t2 > t1 が成り立つようになっています。
派生パラメータ
個別の減衰率:
k1=1/t1
k2=1/t2
k3=1/t3
個別の半減期:
thalf1=t1*ln(2)
thalf2=t2*ln(2)
thalf3=t3*ln(2)
Note: 半減期は通常、慣例により記号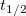 で示されます。 で示されます。
スクリプトでのアクセス法
nlf_expdec3(x,y0,A1,t1,A2,t2,A3,t3)
関数定義ファイル名
FITFUNC\EXPDEC3.FDF
カテゴリー
Origin Basic Functions, Electrophysiology
|