Beta
関数式
![y=y_0+A[1+(\frac{W_2+w_3-2}{w_2-1})(\frac{x-x_c}{w_1})]^{w_2-1}[1-(\frac{w_2+w_3-2}{w_3-1})(\frac{x-x_c}{w_1})]^{w_3-1} y=y_0+A[1+(\frac{W_2+w_3-2}{w_2-1})(\frac{x-x_c}{w_1})]^{w_2-1}[1-(\frac{w_2+w_3-2}{w_3-1})(\frac{x-x_c}{w_1})]^{w_3-1}](//d2mvzyuse3lwjc.cloudfront.net/doc/ja/UserGuide/images/Beta/math-e2072afd0236e2c07c395bb7fe05375b.png)
説明
beta関数
サンプル曲線
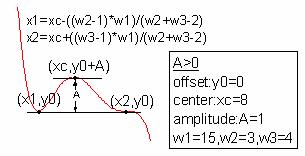
パラメータ
パラメータの数: 6
パラメータの名前: y0, xc, A, w1, w2, w3
意味: y0 = オフセット, xc = 中心, A = 振幅, w1 = 幅, w2 = 幅, w3 = 幅
下側境界: w1 > 0.0, w2 > 1.0, w3 > 1.0
上側境界: なし
スクリプトでのアクセス法
nlf_beta(x,y0,xc,A,w1,w2,w3)
関数定義ファイル名
FITFUNC\BETA.FDF
カテゴリー
Origin Basic Functions, Peak Functions
|