PsdVoigt2
PsdVoigt2-FitFunc
Function
![y=y_0+A\left[ m_u\frac 2\pi \frac{w_L}{4\left( x-x_c\right) ^2+w_L^2}+\left( 1-m_u\right) \frac{\sqrt{4\ln 2}}{\sqrt{\pi}w_G}e^{-\frac{4\ln 2}{w_G^2}\left( x-x_c\right) ^2}\right] y=y_0+A\left[ m_u\frac 2\pi \frac{w_L}{4\left( x-x_c\right) ^2+w_L^2}+\left( 1-m_u\right) \frac{\sqrt{4\ln 2}}{\sqrt{\pi}w_G}e^{-\frac{4\ln 2}{w_G^2}\left( x-x_c\right) ^2}\right]](//d2mvzyuse3lwjc.cloudfront.net/doc/de/UserGuide/images/PsdVoigt2/math-09158df4cd991a056142f67bbb556e22.png)
Brief Description
While Vogit peak
function is the convolution of a Gaussian curve G(x) and a Lorentzian
curve L(x), the Pseudo-Voigt peak function is an approximation of the
Voigt peak function which instead using a linear-combination of Gaussian
curve G(x) and a Lorentzian curve L(x).
Origin provides two types of Pseudo-Vogit peak functions: PsdVogit1 and PsdVogit2.
When using PsdVogit1, you can only specify one FWHM value denoted
as w which will be shared between Gaussian curve G(x) and a Lorentzian
curve L(x); while with PsdVogit2, you can specify two distinct
FWHM values wG for Gaussian curve G(x) and wL for Lorentzian
curve L(x).
Sample Curve
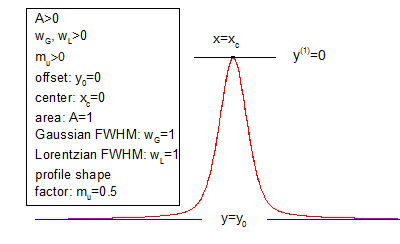
Parameters
Number: 6
Names: y0, xc, A, wG, wL, mu
Meanings: y0 = offset, xc = center, A =area, wG=Gaussian FWHM, wL=Lorentzian
FWHM, mu = profile shape factor
Lower Bounds: wG > 0.0, wL > 0.0
Upper Bounds: none
Script Access
nlf_psdvoigt2(x,y0,xc,A,wG,wL,mu)
Function File
FITFUNC\PSDVGT2.FDF
Category
Spectroscopy
|