fitcmpmodel(Pro)
メニュー情報
モデルの比較
概要
同じデータセット内にある、2つのフィットモデルを比較します。
追加の情報
このコマンドはスクリプトからアクセスできません。これはOrigin Proのみの機能です。
変数
| 表示名 |
変数名 |
I/Oとタイプ |
デフォルト値 |
説明 |
| フィット結果1 |
result1 |
入力
範囲
|
|
異なるモデルで同じデータセットをフィットしたレポートシートを指定します。 |
| フィット結果2 |
result2 |
入力
範囲
|
|
異なるモデルで同じデータセットをフィットしたレポートシートを指定します。 |
| AIC(赤池情報量規準) |
aic |
入力
int
|
1 |
赤池情報量基準(AIC)の結果を比較の為に出力するかどうか指定します。この方法はモデルの比較に関して、制限が少なくなります。 |
| BIC(ベイズ情報量基準) |
bic |
入力
int
|
0 |
ベイズ情報量基準(BIC)の結果を比較の為に出力するかどうか選択して判断します。BICはAICに比べて大きなペナルティが課せられ、これはデータの加重フィットを解決するために使用します。 |
| F検定 |
ftest |
入力
int
|
0 |
F検定の結果を比較の為に出力するかどうか指定します。F検定は階層(ネスト)モデルでないと意味を成しません。 |
| フィットパラメータ |
param |
入力
int
|
1 |
比較に対してフィットパラメータを出力するか判断します。 |
| フィット統計 |
statics |
入力
int
|
1 |
比較に対してフィット統計表を出力するか判断します。 |
| 第1モデル名 |
name1 |
入力
文字列
|
Model1 |
レポートシートの最初のモデルの表示名を指定します。 |
| 第2モデル名 |
name2 |
入力
文字列
|
Model2 |
レポートシートの2つ目のモデルの表示名を指定します。 |
| 結果 |
rt |
出力
ReportTree
|
<新規> |
出力レポートの保存場所を指定します。 |
説明
このツールは同じデータセットに対して、どのフィットが最適かを確認するのに使用できます。
通常、最もよいフィットかどうかを確認するのに、自由度あたりのカイ二乗の値を比較するように習います。これは当てはまりの良さを確認する、とてもよい方法です。数値が1.0に近ければ近いほど、モデルはデータを良く表しています。しかし、それぞれのポイントで分散が入力されるため、カイ二乗の計算値は正確に分かりません。カイ二乗検定は統計的に意味をなさないことになります。
よって、次の2通りの方法でモデル比較を行います。
F検定
F検定は残差の二乗和のそれぞれのモデルの値が異なることを利用して、この値の差からどのモデルが一番いいのかを調べます。F検定は残差の二乗和をよりシンプルなモデルで取り除かれた要素とより複雑なモデルで取り除かれた要素を加えて比較します。よって、2つのモデルが階層(ネスト)しているのは理にかなっています。この方法は次のような状況で使用してください。
1.2つのモデルの数式は同じような構造である必要があります。例えば、
 vs. vs. 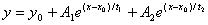
2.パラメータが固定されたモデル vs. パラメータを固定していないモデル
AIC(赤池情報量規準)
赤池情報量基準はどのモデルが最もデータを元に現実的な値を推定できるのか検索します。ネストしたモデルでもネストの無いモデルでも、同時に比較できます。有意に関するコンセプトに依存しないため、AICは最大尤度とランクモデルで構築されています。つまり、AICを元にした不特定要素を追加したモデルでは堅牢で細かい推定結果が取得できます。
このツールを使用するには、次の事に気をつけてください。
- このツールの入力はフィットレポートシート(線形フィット、多項式、非線形曲線フィットなど)です。つまりフィットツールはこのツールを実行する前に行う必要があります。
- レポートシートの最初の結果のみを使用します。つまり、複数のデータセットをフィットする時、それぞれ異なるシートに結果が入力されている事が必要です。
BIC(ベイズ情報量基準)
ベイズ情報量基準はモデルセクションの項目で、Schwarz (1978)に由来します。これはAICのベイズ修正を加えた項目です。BIC検定に課されるペナルティはAIC数式と似ていますが、定数2の代わりにkに対するln(n) を乗数として使い、サンプルサイズnを要素に加えます。 これはデータフィットに関するオーバーフィットの問題を回避できます。
2つのモデルを比較する時、BICの値が低い方がデータによって好まれます。
サンプル
例えば、データセットがありそれにもっともよくフィットするモデルを探したいとします。
比較の候補モデルは次の通りです。
ExpDec1 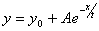
ExpDec2 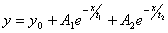
操作
1.\Samples\Curve Fitting フォルダ内にある、 Exponential Decay.dat をインポートします。
2.列Bを選択し、解析:フィット:非線形曲線フィットを選択してダイアログを開きます。関数をExpDec1にセットします。OK をクリックすると結果シートができます。
3.非線形曲線フィットダイアログを再び開き、関数としてはExpDec2をセットします。OK をクリックすると結果シートができます。
4.メニューから、解析:フィット:モデルの比較を選択してダイアログを開きます。
5.参照ボタンをクリックしてレポートツリーブラウザを開き、フィット結果1のために項目を一つ選びます。
6.同じ操作をしてフィット結果2にもう一つの項目を入力します。
7.GUIの中にある全てのオプションを選択してOKをクリックします。
8.F検定表とAIC結果テーブルから、ExpDec1関数が最も良くフィットするモデルだと結論付ける事ができます。
アルゴリズム
1.F検定
F統計量
-
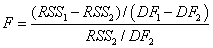
-
- RSS1 はシンプルな方の残差の二乗和で、 RSS2はもう片方のモデルの残差の二乗和です。
確率
-
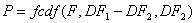
2.AIC(赤池情報量規準)
AIC
-
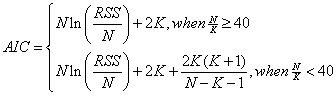
-
- Nはデータポイントの数、Kはパラメータの数+1、RSSはフィットの残差の二乗になります。
重み
-
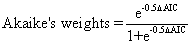
-
- ここで
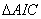 は、2つのAIC値間の差です。 は、2つのAIC値間の差です。
3.Schwarz BIC(ベイズ情報量基準)
BIC
-
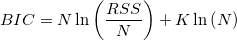
-
- Nはデータポイントの数、Kはパラメータの数+1、RSSはフィットの残差の二乗になります。
-
参考文献
1.Akaike, Hirotsugu (1974). "A new look at the statistical model identification". IEEE Transactions on Automatic Control19 (6): 716-723
2.Burnham, K. R. and D. R. Anderson. 2002. Model Selection and Multimodel Inference. Springer, New York.
関連のXファンクション
fitcmpdata
|