OriginからNAG関数を使った二重積分

サマリー

Origin/OriginProには、「NAG Mark 9」数値ライブラリ完全版が搭載されています。このライブラリを使って、複数の手法で数値積分することができます。全ての関数は、Origin Cからアクセスできます。このチュートリアルでは、NAG関数を呼び出して、二重積分を実行します。ここでは、有限NAG統合を使用します。

学習する項目

このチュートリアルでは、以下の項目について解説します。

• OriginCのNAG関数を呼び出します。
• NAG積分ルーチンを使って、二重積分を解きます。

サンプルとステップ

二重積分を計算するには、NAGライブラリカテゴリーD01 Quadratureの関数を呼び出す必要があります。このカテゴリーには、一次元以上の定積分の数値計算評価を行う関数があります。nag_multid_quad_adapt_1とnag_multid_quad_monte_carlo_1は、異なるアルゴリズムによる二重積分関数で、これら2種類の利用が可能です。このチュートリアルでは、これらを使って、以下の積分を解く方法を学びます。

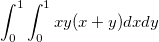
以下のコードの実行とテストの方法については、関連しているチュートリアルOrigin CからNAG関数を呼び出すをご覧ください。コードをコピーして、コードビルダにある新しく作成した「.cファイル」に貼り付けてから、コンパイルとビルドを行います。コメント付Origin Cのコードを以下に示します。

nag_multid_quad_monte_carlo_1を使って

#include <Origin.h>
#include <OC_nag.h> 
#define MAXCLS 20000   //積分評価可能な最大数
double NAG_CALL f(Integer ndim, double x[], Nag_User *comm)  
{
  return x[0]*x[1]*(x[0]+x[1]);  //関数式の定義 
}
int multid_quad_monte_carlo()
{
        Integer exit_status = 0, k, maxcls = MAXCLS, mincls;
        Integer ndim =2;  // 積分の次元数
        
        NagError fail;
        Nag_MCMethod method;
        Nag_Start cont;
        Nag_User comm;
        double a[2], b[2], acc, *comm_arr, eps, finest;         
        comm_arr=NULL;
        
        if (ndim < 1){
                printf("Invalid ndim.\n");
                exit_status = -1;
                return exit_status;   
    } 
        for (k = 0; k < ndim; k++){
                a[k] = 0.0;   // 積分の下限
                b[k] = 1.0;   // 積分の上限
        }
        
        eps = 0.01;  //相対精度
        mincls = 1000; //積分評価の最小数
        method = Nag_ManyIterations;
        cont = Nag_Cold;
        
       /* nag_multid_quad_monte_carlo_1 (d01xbc).
        * Multi-dimensional quadrature, using Monte Carlo method,
        * thread-safe
        */       
nag_multid_quad_monte_carlo_1(ndim, f, method, cont, a, b, &mincls, maxcls,eps, &finest, &acc, &comm_arr, &comm, &fail);
if (fail.code == NE_NOERROR || fail.code == NE_QUAD_MAX_INTEGRAND_EVAL){
        if (fail.code == NE_QUAD_MAX_INTEGRAND_EVAL){
                printf("Error from nag_multid_quad_monte_carlo_1 (d01xbc).\n%s\n",fail.message);
                exit_status = 2;
        }
        //計算結果の出力
        printf("Requested accuracy = %7.2e\n", eps);
        printf("Estimated value = %7.5f\n", finest);
        printf("Estimated accuracy = %7.2e\n", acc);
        printf("Number of evaluations = %6d\n", mincls);     
}
else{
        printf("Error from nag_multid_quad_monte_carlo_1 (d01xbc).\n%s\n",fail.message);
        exit_status = 1;
}
/* 内部に割り当てられたメモリの解放 */
if (comm_arr) 
        NAG_FREE(comm_arr);
return exit_status;
}

次に、LabTalkコンソールの関数を呼び出すと、以下のようになります。

Requested accuracy = 1.00e-002
Estimated value = 0.33326
Estimated accuracy = 2.23e-004
Number of evaluations =   1552

nag_multid_quad_adapt_1を使って

#include <OC_nag.h> 
#include <Origin.h>
#define NDIM 2   //積分次元数
#define MAXPTS 1000*NDIM   //積分評価の最大数
double NAG_CALL f(Integer n, double x[], Nag_User *comm)
{
        return x[0]*x[1]*(x[0]+x[1]);  //関数式の定義 
}
int  multid_quad_adapt()
{
        Integer exit_status = 0;
        Integer ndim = NDIM;
        Integer maxpts = MAXPTS;
        
        double a[2], b[2];
        Integer k;
        double finval;
        Integer minpts;
        double acc, eps;
        Nag_User comm;
        NagError fail;  
        
        for (k = 0; k < 2; k++)
        {
                a[k] = 0.0; //積分の下限
                b[k] = 1.0; //積分の上限
        }     
        eps = 0.001;
        minpts = 0;   
        nag_multid_quad_adapt_1(ndim, f, a, b, &minpts, maxpts, eps, &finval,&acc, &comm, &fail);
        if (fail.code != NE_NOERROR && fail.code != NE_QUAD_MAX_INTEGRAND_EVAL)
        {     
                printf("Error from nag_multid_quad_monte_carlo_1 (d01xbc).\n%s\n",fail.message);
                exit_status = 1;
                return exit_status;
        }     
        //計算結果の出力
        printf("Requested accuracy = %7.2e\n", eps);
        printf("Estimated value = %7.5f\n", finval);
        printf("Estimated accuracy = %7.2e\n", acc); 
        return 0;
}

次に、LabTalkコンソールの関数を呼び出すと、次のようになります。

Requested accuracy = 1.00e-003
Estimated value = 0.33333
Estimated accuracy = 3.33e-016