繰り返し測定のある一元配置分散分析1WayRepeatedMeasuresANOVA
概要
繰り返しのある一元配置の分散分析は、一元配置の分散分析に似ていますが、繰り返し測定データを前提とした従属変数を扱います。この状況では、繰り返しファクターのレベル間の相関があるので、通常の一元配置の分散分析の独立性の前提は無くなります。
一元配置の分散分析と同様、繰り返しのある一元配置の分散分析は、平均が等しいかどうかを調べるのに使用します。これらの平均は、測定差の平均と異なる対象の平均も含まれます。結果は、それぞれ「対象の影響範囲内での検定(Test of Within-Subjects Effect )」および「対象影響間の検定(Test of Between-Subjects Effect )」という表に表示されます。
繰り返し測定のある分散分析にはバランスのとれたサンプルデータ、つまり各レベルで同数の標本数がある必要があります。
必要なOriginのバージョン:Origin 8.6 SR0以降
学習する項目
このチュートリアルでは、以下の項目について解説します。
- 統計解析ダイアログににインデックスされたデータを入力する。
- 繰り返しのある一元配置分散分析を実行する。
- 繰り返しのある二元配置ANOVA解析の結果を読みとく。
ステップ
Originはインデックスデータと素データの両方から繰り返しのある一元配置ANOVAを実行できます。繰り返しのある一元配置ANOVAでインデックスデータモードが使用される場合、データは因子、データ、被験者の3つの列で整理されている必要があります。素データモードを使用する場合、異なるレベルは別の列に入力します。
インデックスデータモード
データは3つの異なる用量を用いて20の被験者から得た計測結果を含んでいます。これから確認したいのは異なる用量を与えた被験者に対して異なる効果を得られたかどうかです。これを検証するには繰り返しのあるインデックスデータモードの一元配置ANOVAを使用して実行します。
- 新しいワークブックを用意します。ヘルプ: フォルダを開く: サンプルフォルダを選択して、サンプルフォルダを開きます。このフォルダ内のStatisticsサブフォルダにあるOne Way_RM_ANOVA_indexed.dat ファイルを探します。空のワークシートにファイルをドラッグアンドドロップしてインポートします。
- メニューから、統計: ANOVA: 一元配置(繰り返し測定)を選択し、ダイアログを開きます。入力データドロップダウンリストからインデックスを選択します。因子、データ、被験者にそれぞれB(dose), C(Data), A(Subject)を選択します。
- 平均比較タブを開き、Bonferroni のチェックを付けてBonferroni検定を有効にします。
- プロットブランチを開き、平均値をプロット(SEをエラーバー表示)と平均比較プロットにチェックを付けます。
- OK ボタンをクリックして、分析を実行します。
結果の読み取り:
ANOVAOneWayRM1ワークシートを開き、分析結果の表を開きます。
繰り返しのある二元配置ANOVAの結果の読み取りについての詳細は、ヘルプファイルを参照してください。
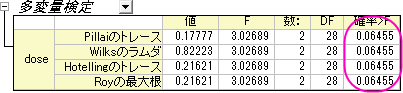
Originは繰り返しのある観測結果と共にMANOVA (多変量分散分析)の出力を行い、繰り返し効果を検出しようとします。4つの異なる手法(Pillaiのトレース, Wilksのラムダ, Hotellingのトレース, Royの最大根)では、まったく同じF検定値と確率、P=0.06455を算出するので、3つのレベル変化による平均は統計的に優位に異ならない、という事ができます。
以下の繰り返しのある分散分析のレポートによると、結論は保守的であるといえます。

この表はMauchlyの球面性検定の結果を記載しています。検定結果から、球面性は維持されている事がわかります。ここで探している値は、 Mauchly'検定が有意水準にある事をしめす、確率がカイ二乗より大きい(Prob > ChiSq)値なので、この例の中では有意水準l (0.44609)は0.05よりも大きい事を示します。つまり、球面性の仮定は棄却できないことを示します。
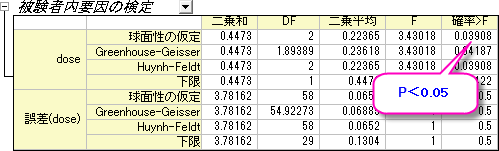
この表からは因子についてのF値と共に、その値の有意水準と効果サイズを得る事ができます。データが球面性を持つという仮定に則っているので、球面性を仮定して行われた繰り返しのある一元配置ANOVAから得た結果は、これら3つの条件のもとで得られた平均は統計的に有位に異なる(P = 0.03908 < 0.05より)、という事です。言い換えると、dose(用量)は有意要因である、といえます。
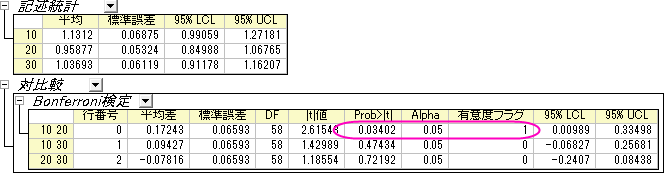
先の表で提示された結果では、平均間では全体的に有意差はありましたが、これらの差がどこから来たのか分かりません。この表はBonferroni検定の結果を表示します。これにより、どの平均が異なっていたのかを見る事ができます。この場合、dose1とdose2の平均は有意に異なっていたといえます(P = 0.03402 < 0.05、有意度pフラグ=1より)。
以下の2つのプロットからも同じような結論を導き出すことができます。
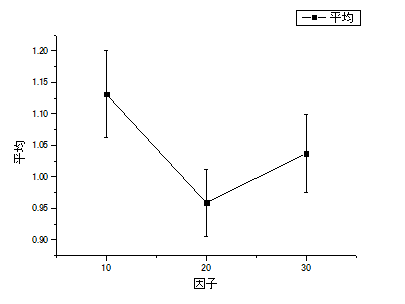 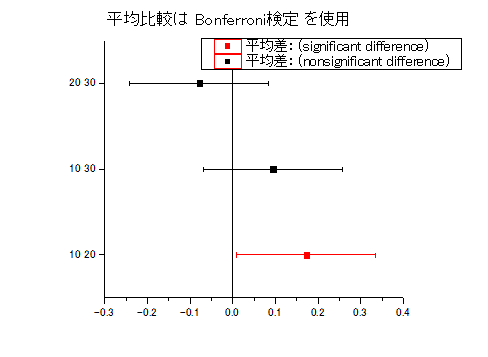
|