信号処理

Signal-Processing

グラフ内のデータセットのスムージング

次のサンプルでは、アクティブレイヤにプロットされたすべてのデータをスムージングします。スムージング後のデータは新しいブックに出力されます。

// レイヤ内のデータプロットの数を数える
//結果は変数"count"に入る "count"
layer -c; 
string gname$ = %H;   // グラフページの名前を取得
// smoothed という名前で新しいワークブックを作成 
//名前はbkname$に入る
newbook na:=Smoothed; 
wks.ncols=0;          // 列なしで開始
loop(ii,1,count) {
    // 入力範囲はii番目のプロット
    range riy = [gname$]!$(ii);    
    // 出力範囲は新しい2列            
    range roy = [bkname$]!($(ii*2-1),$(ii*2));
   // 3次多項式を使用したSavitsky-Golayスムージング
    smooth iy:=riy meth:=sg poly:=3 oy:=roy;   
}

包絡線（Proのみ）

以下のスクリプトは、Xファンクションenvelopeを使用して、信号の上下の包絡線を検索します。

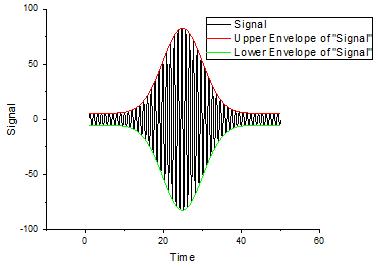
//ガウスの包絡線を持つ信号をインポート
fname$ = system.path.program$ + "samples\signal processing\Gaussian Envelope.dat";
impasc;
envelope iy:=col(2) type:=both;
//作図
plotxy iy:=(?,1:6) plot:=200;

欠損値のあるデータのFFT

OriginのFFT機能では、入力データに欠損値がないことを前提としています。そのため、FFTするデータに欠損値がある場合、何か値を入れる必要があります。簡単なのは、単純な線形補間を実行し、欠損している部分の値を得ることです。

このサンプルでは、欠損値を含む11年の太陽黒点周期を表す2つのデータ範囲について、線形補間し、FFT振幅をプロットします。

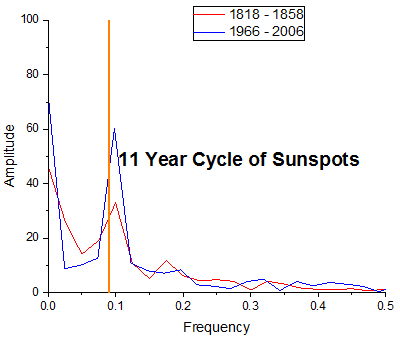
// データをインポート
string fname$ = system.path.program$ + "Samples\Signal Processing\dayssn.dat";
//col(1) = 年, col(2)= 月, col(3)= 日, 
//col(4) = 日付の値（1年を1とする）
//col(5) = 観測データ
//col(4)=X、col(5)=Yとして5列必要
newbook s:=0;newsheet cols:=5 xy:="NNNXY"; 
impasc;

// 欠損値を補間して、結果をcol(6)に入れる
interp1q 4 (4,5) 6;
// このデータを使う
range rData1 = 6[1:14609];// 1818から1858年
range rData2 = 6[54057:end];// 1966から2006年
// Xファンクションfft1を使ってFFT 
// ReportDataシートとReportTableシートが作成される
fft1 rData1;
//Xファンクション実行後同じ名前のツリーが作成される
//ReportDataノードのfft1.rd を使う
range rReportData1=fft1.rd$;//FFT結果からのReport Dataを保持
range rAmp1=%(rReportData1.getlayer()$)col(Amplitude);
rAmp1[C]$="1818 - 1858"; // グラフ凡例に適切なコメントに変更

fft1 rData2;
range rReportData2=fft1.rd$;
range rAmp2=%(rReportData2.getlayer()$)col(Amplitude);
rAmp2[C]$="1966 - 2006";

// 空のグラフウィンドウを開く。必要に応じて自身のテンプレートを使用
win -t plot;
// 結果をアクティブグラフレイヤにプロット
plotxy rAmp1 plot:=200 color:=color(red) o:=<active>;
plotxy rAmp2 plot:=200 color:=color(blue) o:=<active>;
// ピークを表示するために拡大
x1=0;x2=0.5;y1=0;y2=100;
// 11年に垂直線で印をつける
draw -n peakval -l -v 1/11; 
peakval.linewidth = 3;
peakval.color = color(orange);
// テキストラベルを追加
label -n peaklabel \b(11 Year Cycle of Sunspots);
peaklabel.x = peakval.x + 1.1 * peaklabel.dx / 2;
peaklabel.y = (y1 + y2) / 2;
peaklabel.fsize = 30;

FFT結果の基本統計量を計算

FFT結果を元にした最大振幅および対応する周波数、平均周波数、メディアン周波数といった基本統計量を計算します。このサンプルでは、統計量を計算する際に途中で算出される内容は表示しません。

fname$ = system.path.program$ + "Samples\Signal Processing\Signal with Discrete Frequencies.dat";
newbook;
impasc;
 
Tree myfft;// 全てのツリー変数を確認するのに"list vt"を使用できる
// "myfft"ツリーにFFT結果を出力
//ツリー構造を確認するときは"myfft.="を実行
fft1 ix:=2 rd:=myfft rt:=<none>;
dataset tmp_x=myfft.fft.freq; // ツリーのベクトルノードはどんなデータセットも割り当て可能
dataset tmp_y=myfft.fft.amp;
 
diststats iy:=(tmp_x, tmp_y);
type "For data from %(fname$)";
type "the mean frequency is $(diststats.mean)";

2つの信号のコンボリューションを算出（Proのみ）

OriginProでは、Xファンクションconvを使って2つの信号のコンボリューションを算出できます。

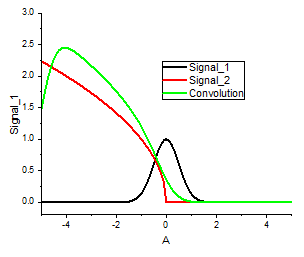
newbook s:=0 name:=Convolution;
newsheet cols:=3 xy:="XYY";
//コンボリューションする2つの信号をセットアップ
Col(1)=Data(-5,10,0.1);
Col(2)=exp(-col(1)^2*2);   
Col(3)=(Col(1)<0)?sqrt(-Col(1)):0;
col(2)[L]$ = "Signal_1";
col(3)[L]$ = "Signal_2";
//signal_1とsignal_2のコンボリューションを計算
conv ix:=Col("Signal_1") response:=Col("Signal_2") interval:=0.1 circular:=circular oy:=<new>!(<new>,<new>);

range rr=[Convolution]2!1; // 元の信号に一致させるX
rr=rr-10;
range rc=[Convolution]2!2; 
rc=rc*0.1;   //コンボリューション結果にサンプリング間隔0.1をかける
rc[L]$="Convolution";

//グラフに結果をプロット
plotxy (1!(1,2),1!(1,3),2!(1,2)) plot:=200;

layer.x.from=-5;
layer.x.to=5;
layer.y.from=-0.2;
layer.y.to=3;
set %C -w 1500;

ヒルベルト変換（Proのみ）

以下のLabTalkスクリプトは、XファンクションHilbertを使ったヒルベルト変換の計算を行います。そして、SetおよびGetコマンドを使って結果を投影付きの3D線グラフとしてプロットします。

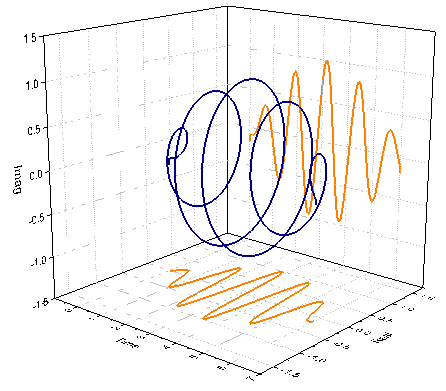
newbook sheet:=0 name:=Hilbert1;
newsheet cols:=2 xy:="XY";

//データをセットアップ
Col(1)=Data(0,6,0.02);
Col(2)=sin(5*col(1))*sin(0.5*col(1)); 
 
//ヒルベルト変換
hilbert ix:=[Hilbert1]1!2 rd:=[<input>]1!<new>;
wks.nCols = wks.nCols + 2;
wks.col6.type=6;
Col(5)=ImReal(Col(4));
Col(6)=Imaginary(Col(4));

//列ロングネームを設定
col(1)[L]$ = "Time";
col(5)[L]$ = "Real";
col(6)[L]$ = "Imag";

//ヒルベルト変換の結果を3Dグラフにプロット
plotxyz iz:=(1,5,6) plot:=240;

//複素信号の線とシンボルを設定
set %C -so -lo 0; // Z方向のドロップラインを非表示
set %C -so -l 1;  // シンボルを線で接続
set %C -so -w 1500; // 線の幅を設定
set %C -so -cl 9; // 線の色をネイビーにする
set %C -so -z 0; // シンボルサイズは0にして非表示

set %C -sz -s 1; // XY投影を表示
set %C -sz -l 1; // シンボルを線で接続
set %C -sz -z 0; // シンボルサイズを0にして非表示
set %C -sz -w 1500; // 線の幅を設定
set %C -sz -cl 15; // 線の色を橙色にする

set %C -sy -s 1; // XZ投影を表示
set %C -sy -l 1; // シンボルを線で接続
set %C -sy -z 0; // シンボルサイズを0にして非表示
set %C -sy -w 1500; // 線の幅を設定
set %C -sy -cl 15; // 線の色を橙色にする

//軸範囲を設定
layer.x.from-=0.5;
layer.y.from-=0.5;
layer.z.from-=0.5;
layer.x.to+=0.5;
layer.y.to+=0.5;
layer.z.to+=0.5;