Übersicht Nicht-parametrische Statistik
NonparametricStatisticsOverview
Zusammenfassung
Nicht-parametrische Tests werden verwendet, wenn Sie nicht wissen, ob Ihre Daten einer Normalverteilung folgen, oder Sie bestätigt haben, dass Ihre Daten keiner Normalverteilung folgen.
Was Sie lernen werden
Dieses Tutorial zeigt Ihnen:
- Eine Einführung in nicht-parametrische Tests in Origin
- Das Ausführen von nicht-parametrischen Tests für unterschiedliche praktische Situationen
- Das Berechnen des Korrelationskoeffizienten in nicht-parametrischen Statistiken
Einführung: Nicht-parametrische Tests in Origin
Nicht-parametrische Tests erfordern keine Annahme einer Normalverteilung. Sie werden gemeinhin in den folgenden Situationen verwendet:
- Kleiner Stichprobenumfang
- Kategoriale/Binäre/Ordinale Daten
- Normalverteilung kann nicht angenommen werden.
|
|
Nichtparametrisch |
Parametrisch |
|
|
Daten aus einer beliebigen Verteilung |
Daten aus einer Normalverteilung |
| Kleine Stichprobe |
Große Stichprobe |
| Eine Stichprobe |
|
Wilcoxon-Rangtest mit Vorzeichen |
t-Test bei einer Stichprobe |
| Zwei Stichproben |
Unabhängige Stichproben |
- Mann-Whitney-Test
- Kolmogorov-Smirnov-Test
|
t-Test bei zwei Stichproben |
| Verbundene Stichproben |
- Wilcoxon-Rangtest mit Vorzeichen
- Vorzeichentest
|
t-Test bei verbundenen Stichproben |
| Mehrere Stichproben |
Unabhängige Stichproben |
- Kruskal-Wallis-ANOVA
- Mood-Median-Test
|
Einfache ANOVA |
| Verwandte Stichproben |
Friedman-ANOVA |
Einfache ANOVA mit wiederholten Messungen |
Beispiele
Tests bei einer unabhängigen Stichprobe
Der Wilcoxon-Rangtest mit Vorzeichen bei einer Stichprobe wurde entwickelt, um den Median einer Grundgesamtheit im Verhältnis zu einem festgelegten Wert zu untersuchen. Sie können dazu einen ein- oder beidseitigen Test wählen. Die Hypothesen des Wilcoxon-Rangtests mit Vorzeichen sind H0: Median = hypothetischer Median vs. H1: Median ≠ hypothetischer Median.
In diesem Beispiel interessiert sich ein Qualitätsingenieur in einem Betrieb dafür, ob der Median (oder Durchschnitt) des Produktgewichts gleich 166 ist. Zunächst werden zufällig 10 Produkte ausgewählt und ihr Gewicht gemessen. Die gemessenen Daten lauten:
151,5 152,4 153,2 156,3 179,1 180,2 160,5 180,8 149,2 188,0
Der Ingenieur führt einen Test auf Normalverteilung durch, um zu bestimmen, ob die Daten einer Normalverteilung folgen
- Öffnen Sie ein neues Arbeitsblatt und geben Sie die oben stehende Daten in Spalte A ein. Wählen Sie Statistik: Deskriptive Statistik: Test auf Normalverteilung... , um den Dialog Test auf Normalverteilung zu öffnen.
- Wählen Sie die Spalte A(X) als Datenbereich.
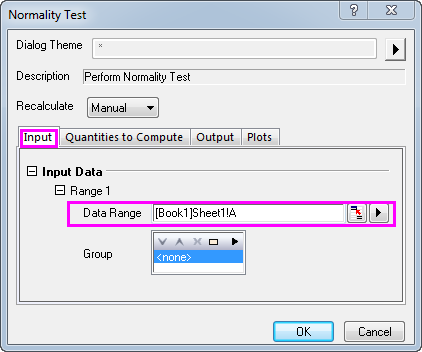
- Klicken Sie auf die OK, um die Ergebnisse zu erzeugen.

Von dem Ergebnis ausgehend, das den p-Wert = 0,03814 ausgibt, ist die Verteilung der Daten nicht normalverteilt bei einem Niveau von 0,05. Um einen Wilcoxon-Rang-Test mit Vorzeichen bei einer Stichprobe durchzuführen:
- Wählen Sie Statistik: Nicht-parametrische Tests: Wilcoxon-Rangtest mit Vorzeichen bei einer Stichprobe.
- Legen Sie Spalte A als Datenbereich fest.
- Geben Sie 166 im Textfeld Testmedian ein.
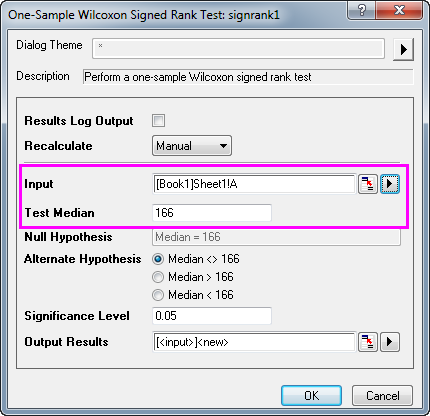
- Klicken Sie auf die OK, um die Ergebnisse zu erzeugen.

Gemäß dem Ergebnis wird die Nullhypothese bei einem Niveau von 0,05 zurückwiesen und geschlussfolgert, dass der Median gleich 166 ist.
Tests bei zwei unabhängigen Stichproben
Origin bietet zwei Tests für nicht-parametrische Statistiken von zwei unabhängigen Stichprobensystemen: den Mann-Whitney-Test und den Kolmogorov-Smirnov-Test bei zwei Stichproben.
Dieses folgende Beispiel zeigt die praktische Verwendung des Mann-Whitney-Tests. Die Abriebfestigkeit (in mg) wird für zwei Reifentypen (A und B) gemessen, wobei 8 Versuche für jeden Reifentypen durchgeführt werden. Die Daten sind indiziert und werden in der Datei abrasion_indexed.dat gespeichert.
- Importieren Sie die Datei abrasion_indexed.dat aus \Samples\Statistics\.
- Wählen Sie Statistik: Nicht-parametrische Tests: Mann-Whitney-Test, um das Dialogfeld zu öffnen.
- Behalten Sie als Form der Eingabedaten die Option Indiziert bei.
- Legen Sie Spalte A als Gruppenbereich fest und die Spalte B als Datenbereich.
- Aktivieren Sie das Kontrollkästchen Genauer p-Wert.
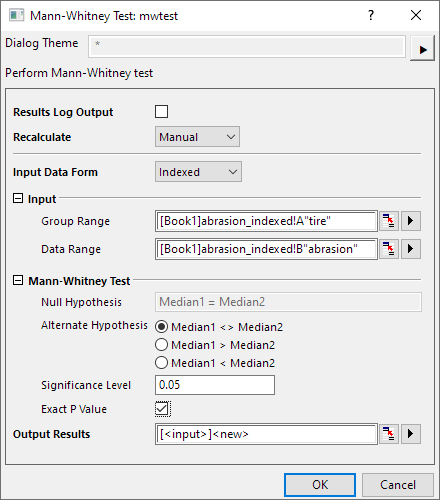
- Klicken Sie auf die Schaltfläche OK, um Ergebnisse zu erzeugen, die sich im Blatt MannWhitney1 befinden.
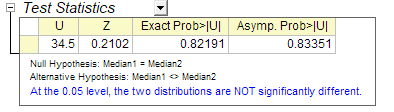
- U: Die U-Statistik kann einfach aus dem Rang der zwei Gruppen berechnet werden. Es handelt sich hier um die Anzahl der Male, die ein Score in der 2. Gruppe größer ist als ein Score in der 1. Gruppe.
- Z: Die approximative Statistik des Tests auf Normalverteilung. Sie bietet eine hervorragende Approximation mit wachsender Stichprobengröße.
- Genaue Wahrsch: Der genaue P-Wert, der nur verfügbar ist, wenn Genauer p-Wert im Dialog aktiviert ist. Er kann jedoch sehr viel CPU-Zeit in Anspruch nehmen, wenn große Stichprobenumfänge bearbeitet werden.
- Asymp. Wahrsch.: Der asymptotische p-Wert wird aus der approximativen Statistik des Tests der Normalverteilung Z berechnet.
Nicht-parametrische Messungen der Korrelation
Der Korrelationskoeffizient wird zur Messung der Beziehung zwischen zwei Variablen verwendet. Es ist möglich, den Korrelationskoeffizienten für eine nicht-parametrische Statistik zu verwenden.
Origin bietet zwei nicht-parametrische Methoden zum Messen der Korrelationen zwischen Variablen:
- Spearman: Häufige verwendete Alternative zu Pearsons Korrelationskoeffizient. Spearmans Koeffizient kann verwendet werden, wenn sowohl die abhängige als auch die unabhängige Variable ordinal ist oder wenn eine Variable ordinal und die andere kontiniuerlich ist. Spearmans Koeffizient kann jedoch auch geeignet sein, wenn beide Variablen kontinuierlich sind.
- Kendall: Wird mit ordinalen Variablen zum Auswerten von Übereinstimmungen unter Prüfern verwendet.
Das folgende Beispiel zeigt, wie der Korrelationskoeffizient für nicht-parametrische Situationen berechnet wird.
- Importieren Sie die Datei abrasion_raw.dat aus \Samples\Statistics\.
- Markieren Sie Spalte A und Spalte B. Wählen Sie Statistik: Deskriptive Statistik: Korrelationskoeffizient, um den Dialog corrcoef zu öffnen.
- Aktivieren Sie Spearman und deaktivieren Sie Pearson.
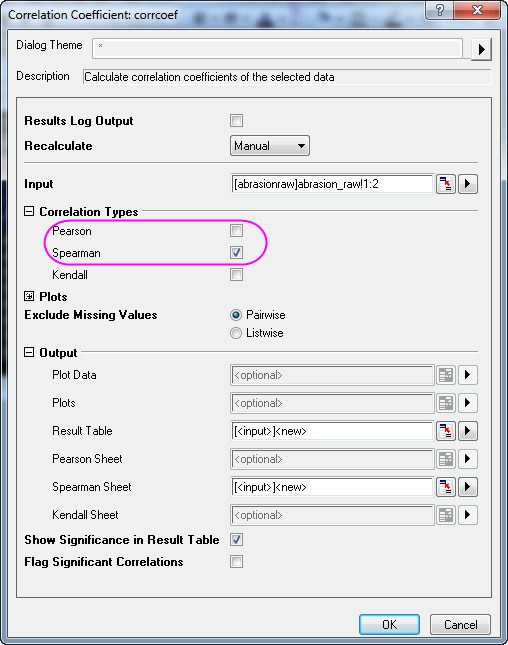
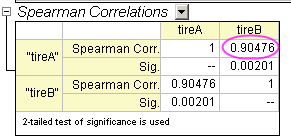
- Klicken Sie auf die Schaltfläche OK, um die Ergebnisse in dem Blatt CorrCoef1 zu erzeugen.
Aus dem Wert von Spearman Corr. kann geschlussfolgert werden, dass der Abrieb zwischen Reifen A und Reifen B stark miteinander korreliert.
Wilcoxon-Vorzeichen-Rang-Test bei verbundenen Stichproben
Nun werden die zwei Mediane von Reifen A und Reifen B aus dem obenstehenden Beispiel verglichen.
- Arbeiten Sie weiterhin mit der Datei abrasion_raw.dat aus \Samples\Statistics\.
- Wählen Sie Statistik: Nicht-parametrische Tests: Wilcoxon-Rangtest mit Vorzeichen bei verbundenen Stichproben.
- Legen Sie Spalte A als Ersten Datenbereich fest und Spalte B als Zweiten Datenbereich.
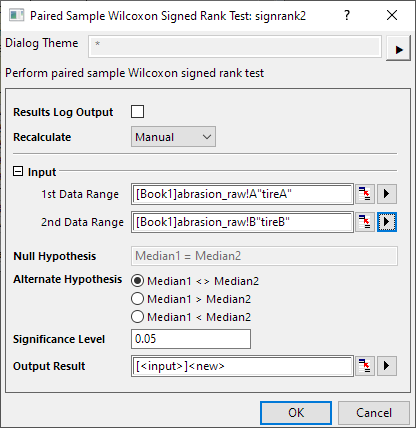
- Klicken Sie auf die Schaltfläche OK, um die Ergebnisse zu erzeugen.
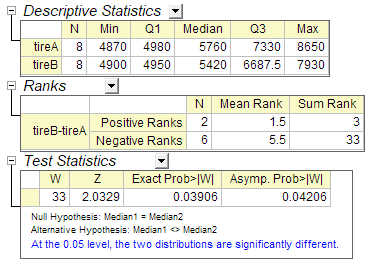
Sie können schlussfolgern, dass die zwei Mediane signifikant unterschiedlich sind. Der Median von Gruppe A ist größer als der Median von Gruppe B.
Test bei mehreren unabhängigen Stichproben
In diesem Beispiel wird der Kraftstoffverbrauch von vier Autoherstellern gemessen. Es werden mehrere Versuche für jeden Autohersteller durchgeführt. Die Ergebnisse werden in der Beispieldatentabelle aufgeführt.
| GMC/mpg |
Infinity/mpg |
Saab/mpg |
Kia/mpg |
| 26,1 |
32,2 |
24,5 |
28,4 |
| 28,4 |
34,3 |
23,5 |
34,2 |
| 24,3 |
29,5 |
26,4 |
29,5 |
| 26,2 |
35,6 |
27,1 |
32,2 |
| 27,8 |
32,5 |
29,9 |
|
| 30,6 |
30,2 |
|
|
| 28,1 |
|
|
|
Um auszuwerten, ob der Kraftstoffverbrauch von vier Autoherstellern gleich ist und welche Marke die effektivste, wird die Kruskal-Wallis-ANOVA als nicht parametrische Testmethode ausgewählt.
- Erstellen Sie eine neue Arbeitsmappe in Origin, kopieren Sie die Beispieldaten und fügen Sie sie ein.
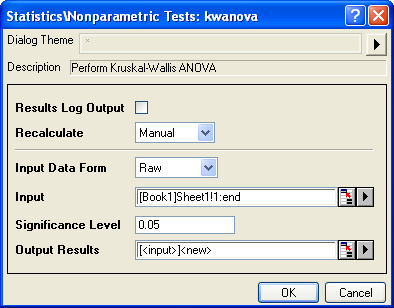
- Wählen Sie Statistik: Nicht-parametrische Tests: Kruskal-Wallis-ANOVA, um das Dialogfeld kwanova zu öffnen.
- Wählen Sie Roh als Form der Eingabedaten.
- Klicken Sie auf die dreieckige Schaltfläche
 neben Eingabe und klicken Sie dann auf Alle Spalten im Kontextmenü. neben Eingabe und klicken Sie dann auf Alle Spalten im Kontextmenü.
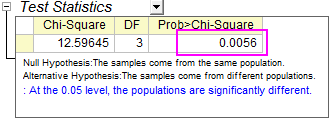
- Klicken Sie auf OK, um Ergebnisse zu erzeugen. Die Ergebnisse werden in einem neuen Arbeitsblatt KWANOVA1 gespeichert.
Der P-Wert lässt uns schlussfolgern, dass der Kraftstoffverbrauch der vier Autohersteller sich signifikant voneinander unterscheidet.
Test bei mehreren verwandten Stichproben
Augenärzte untersuchen, ob eine Helium-Neon-Laser-Therapie bei Kindern angewendet werden kann. Sie haben Daten von 2 Gruppen, 6-10 Jahre und 11-16 Jahre. Jeder Datensatz enthält die Untersuchungsergebnisse von 5 Personen und den Differenzen in ihrer Sehkraft nach drei Therapiezyklen. Die Ergebnisse werden in der Datei eyesight.dat gespeichert.
Aufgrund des kleinen Stichprobenumfangs ist eine nicht-parametrische Statistik in der Analyse erforderlich. Befolgen Sie bitte die untenstehenden Schritte:
- Importieren Sie die Datei eyesight.dat aus \Samples\Statistics\.
- Wählen Sie Statistik: Nicht parametrische Tests: Friedman-ANOVA, um das Dialogfeld friedman zu öffnen.
- Wählen Sie Spalte A als Datenbereich, Spalte C als Faktorbereich und Spalte D als Subjektbereich.
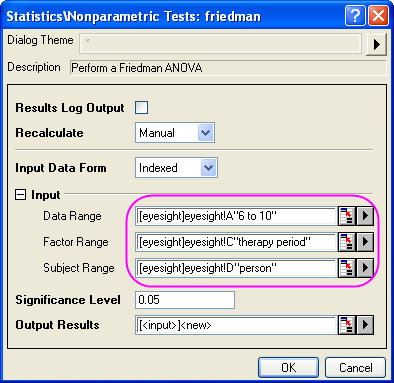
- Klicken Sie auf die OK, um die Ergebnisse zu erzeugen.
Der p-Wert von 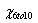 ist 0,0067379, also weniger als 0,05. Die Grundgesamtheiten sind signifikant unterschiedlich und weisen damit darauf hin, dass die Therapie für die Altersgruppe 6-10 wirksam ist. ist 0,0067379, also weniger als 0,05. Die Grundgesamtheiten sind signifikant unterschiedlich und weisen damit darauf hin, dass die Therapie für die Altersgruppe 6-10 wirksam ist.
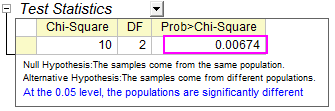
Auf ähnliche Weise wählen Sie Spalte B als Datenbereich. Die verbleibenden Einstellungen der Eingabe entsprechen denen aus Schritt 3 oben.
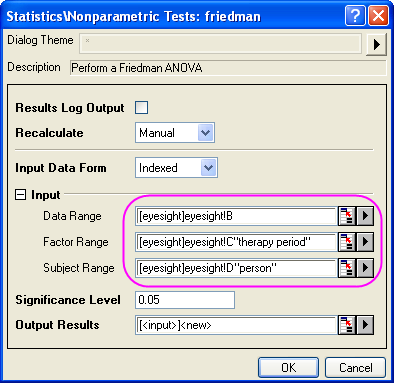
Überprüfen Sie das Ergebnis. Es ist zu sehen, dass der p-Wert von 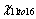 0,02599 beträgt, weniger als 0,05 oder 0,10. Daher können Sie schlussfolgern, dass die Sehkraft von 11-16-jährigen Personen nach drei Therapiezyklen besser ist. 0,02599 beträgt, weniger als 0,05 oder 0,10. Daher können Sie schlussfolgern, dass die Sehkraft von 11-16-jährigen Personen nach drei Therapiezyklen besser ist.
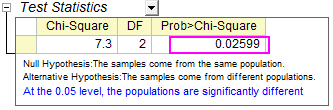
Außerdem ist zu sehen, dass 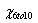 > >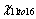 , d.h., die He-Ne-Laser-Therapie funktioniert besser bei Kindern im Alter von 6 bis 10. Je früher Kinder mit der Therapie beginnen, desto mehr kann sich ihre Sehkraft verbessern. , d.h., die He-Ne-Laser-Therapie funktioniert besser bei Kindern im Alter von 6 bis 10. Je früher Kinder mit der Therapie beginnen, desto mehr kann sich ihre Sehkraft verbessern.
|