4.4 NLFit and Peak Analyzer
Python functions can be used for performing nonlinear curve fitting. Peak functions defined with Python can also be used in Peak Analyzer. A fitting function file (FDF file) will need to be created which includes the Python function and script commands to install any Python packages that are needed for your Python function.
The following example outlines how to create an FDF with Python function.
Fitting Function for Mass Diffusion
This section outlines the procedure to create a fitting function for the Mass Diffusion equation:
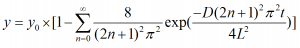
using a Python function.
- First we need to create a new FDF file. Open the Fitting Function Builder tool using the Origin menu Tools: Fitting Function Builder...
- On the first page, select Create a New Function.
- On the second page, set Function Name to MassDiffusion, then select Python Function(Vector) for function type.
- On the third page, set independent variables to x, dependent variables to y, and set parameters to y0, D, L
- On the fourth page, enter
from mpmath import nsum, exp, inf
import numpy as np
def MassDiffuse(x, y0, D, L):
sm = [float((nsum(lambda ii: 1/(2*ii+1)**2*exp(-D*(2*ii+1)**2*np.pi**2*t/(4*L**2)),[0, inf]))) for t in x]
return [y0*(1-8/np.pi**2*t) for t in sm]
in the Python Function(Vector) edit box. Enter
y = MassDiffuse(x, y0, D, L)
in the Function Body edit box.
- On the fifth page, enter
if(Python.chk("mpmath numpy") > 1)
return 1;
return 0;
in the Python Package Check(Labtalk Script) edit box. This function requires the mpmath and numpy packages. These need to be installed prior to using the function. To install the packages, you can use the Python Packages tool accessible from the Connectivity menu in Origin. When you share the function with another colleague, the packages can be automatically installed when that user adds the function to their Origin.
- Click Next button then click Finish button.
- You can test the fitting function with the following data for X and Y:
0.00 -0.078
0.20 0.604
0.40 0.842
0.60 1.101
0.80 1.029
1.00 1.083
1.20 0.828
1.40 0.884
1.60 0.991
1.80 1.005
2.00 0.915
Then use the initial parameter values:
y0 = 1, D = 0.5, L = 0.5
and perform the fitting. The final parameter results will be:
Fitted values: y0 = 0.97846, D = 0.37563, L = 0.43781
Evaluate FDF in Python code
This shows how to define a fitting function with evaluate FDF in Python code.
- First we need to create a new FDF file. Open the Fitting Function Builder tool using the Origin menu Tools: Fitting Function Builder...
- On the first page, select Create a New Function.
- On the second page, set Function Name to HgPyEx, then select Python Function(Vector) for Function Type.
- On the third page, set Independent Variables to x, Dependent Variables to y.
Set Parameters to:
dx196,dx198,dx199,dx200,dx201,dx202,Vbl,Vamp,a1V,a2V,wLor,dFwm,fshift,P,T,L,nA
set Derived Parameters to:
ConcRef,wLorPval,fshiftPval
- On the fourth page in Parameters tab, set the values to coressponding parameters:
Names = Vbl,Vamp,a1V,a2V,wLor,dFwm,fshift,P,T,L,nA
Initial Values = 0(F),0.99629(V),0.000231(V),0(F),8.54(F),1(V),-2.54(F),1(F),1(F),89.87071(F),1.15e-05(V)
Number Of Significant Digits = 0,0,0,0,6,7,6,0,0,0,15
Unit = ,,,,MHz/Torr,,MHz/Torr,,,,
In the Python Function(Vector) edit box, enter
import numpy as np
import originpro as op
def Voigt(x, xc, A, alpha, gamma):
"""
Return the Voigt line shape at x with Lorentzian component FWHM gamma
and Gaussian component FWHM alpha.
"""
#vp = ['y0','xc','A','wG','wL']
va = [0, xc, A, alpha, gamma]
x1=x.tolist()
return np.array( op.evaluate_FDF( 'Voigt', x1, va ) )
def HgOFunc( x, dx196, dx198, dx199, dx200, dx201, dx202, Vbl, Vamp, a1V, a2V, wLor, dFwm, fshift, P, T, L, nA):
# define transition frequencies
f1 = 1181.55994207E3
f2 = 1181.55583492E3
f3 = 1181.54042558E3
f4 = 1181.56256226E3
f5 = 1181.55102924E3
f6 = 1181.54117507E3
f7 = 1181.55515739E3
f8 = 1181.56270616E3
f9 = 1181.54573191E3
f10 = 1181.54052152E3
f1_9 = 0
f2_9 = 0
f3_9 = 0
f4_9 = 0
f5_9 = 0
f6_9 = 0
f7_9 = 0
f8_9 = 0
f9_9 = 0
f10_9 = 0
Pval=P
wLorP=wLor*P/1000 # units GHz = MHz/Torr*Torr/1000
fshiftP=fshift*P/1000 # units GHz = MHz/Torr*Torr/1000
#x=x+f9+dFwm
vx = np.array( x )
vx = vx+f9+dFwm
m196 = 195.96581
m198 = 197.96674
m199 = 198.96825
m200 = 199.96825
m201 = 200.97028
m202 = 201.97062
m204 = 203.97347
'''
w1 = 7.162326E-07*f1*(T/m196)^0.5
w2 = 7.162326E-07*f2*(T/m198)^0.5
w3 = 7.162326E-07*f3*(T/m199)^0.5
w4 = 7.162326E-07*f4*(T/m199)^0.5
w5 = 7.162326E-07*f5*(T/m200)^0.5
w6 = 7.162326E-07*f6*(T/m201)^0.5
w7 = 7.162326E-07*f7*(T/m201)^0.5
w8 = 7.162326E-07*f8*(T/m201)^0.5
w9 = 7.162326E-07*f9*(T/m202)^0.5
w10= 7.162326E-07*f10*(T/m204)^0.5
'''
w1 = 7.162326E-07*f1*(T/m196)**0.5
w2 = 7.162326E-07*f2*(T/m198)**0.5
w3 = 7.162326E-07*f3*(T/m199)**0.5
w4 = 7.162326E-07*f4*(T/m199)**0.5
w5 = 7.162326E-07*f5*(T/m200)**0.5
w6 = 7.162326E-07*f6*(T/m201)**0.5
w7 = 7.162326E-07*f7*(T/m201)**0.5
w8 = 7.162326E-07*f8*(T/m201)**0.5
w9 = 7.162326E-07*f9*(T/m202)**0.5
w10= 7.162326E-07*f10*(T/m204)**0.5
g1 = 3
g2 = 3
g3 = 1
g4 = 2
g5 = 3
g6 = 1.5
g7 = 1
g8 = 0.5
g9 = 3
g10 = 3
x196 = 0.0015 + dx196
x198 = 0.1004 + dx198
x199 = 0.1694 + dx199
x200 = 0.2314 + dx200
x201 = 0.1317 + dx201
x202 = 0.2974 + dx202
x204 = (1 - x196-x198-x199-x200-x201-x202)
'''dF1=x-f1-fshiftP;
dF2=x-f2-fshiftP;
dF3=x-f3-fshiftP;
dF4=x-f4-fshiftP;
dF5=x-f5-fshiftP;
dF6=x-f6-fshiftP;
dF7=x-f7-fshiftP;
dF8=x-f8-fshiftP;
dF9=x-f9-fshiftP;
dF10=x-f10-fshiftP;'''
dF1=vx-f1-fshiftP
dF2=vx-f2-fshiftP
dF3=vx-f3-fshiftP
dF4=vx-f4-fshiftP
dF5=vx-f5-fshiftP
dF6=vx-f6-fshiftP
dF7=vx-f7-fshiftP
dF8=vx-f8-fshiftP
dF9=vx-f9-fshiftP
dF10=vx-f10-fshiftP
'''A1 = (g1*x196/f1^2)*nlf_Voigt(dF1,0,f1_9,1,w1,wLorP) + (g2*x198/f2^2)*nlf_Voigt(dF2,0,f2_9,1,w2,wLorP) + (g3*x199/f3^2)*nlf_Voigt(dF3,0,f3_9,1,w3,wLorP);
A2 = (g4*x199/f4^2)*nlf_Voigt(dF4,0,f4_9,1,w4,wLorP) + (g5*x200/f5^2)*nlf_Voigt(dF5,0,f5_9,1,w5,wLorP) + (g6*x201/f6^2)*nlf_Voigt(dF6,0,f6_9,1,w6,wLorP);
A3 = (g7*x201/f7^2)*nlf_Voigt(dF7,0,f7_9,1,w7,wLorP) + (g8*x201/f8^2)*nlf_Voigt(dF8,0,f8_9,1,w8,wLorP) + (g9*x202/f9^2)*nlf_Voigt(dF9,0,f9_9,1,w9,wLorP);
A4 = (g10*x204/f10^2)*nlf_Voigt(dF10,0,f10_9,1,w10,wLorP);'''
A1 = (g1*x196/f1**2)*Voigt(dF1,f1_9,1,w1,wLorP) + (g2*x198/f2**2)*Voigt(dF2,f2_9,1,w2,wLorP) + (g3*x199/f3**2)*Voigt(dF3,f3_9,1,w3,wLorP)
A2 = (g4*x199/f4**2)*Voigt(dF4,f4_9,1,w4,wLorP) + (g5*x200/f5**2)*Voigt(dF5,f5_9,1,w5,wLorP) + (g6*x201/f6**2)*Voigt(dF6,f6_9,1,w6,wLorP)
A3 = (g7*x201/f7**2)*Voigt(dF7,f7_9,1,w7,wLorP) + (g8*x201/f8**2)*Voigt(dF8,f8_9,1,w8,wLorP) + (g9*x202/f9**2)*Voigt(dF9,f9_9,1,w9,wLorP)
A4 = (g10*x204/f10**2)*Voigt(dF10,f10_9,1,w10,wLorP)
# y value
#y = (Vbl + (Vamp + a1V*dF9 + a2V*dF9^2))*exp(-(nA*L*(2.99792458E8)^2*(1/(8*3.14159265358979))*(A1+A2+A3+A4)));
y = (Vbl + (Vamp + a1V*dF9 + a2V*dF9**2))*np.exp(-(nA*L*(2.99792458E8)**2*(1/(8*3.14159265358979))*(A1+A2+A3+A4)))
return y.tolist()
In the Function Body edit box, enter
y=HgOFunc( x, dx196, dx198, dx199, dx200, dx201, dx202, Vbl, Vamp, a1V, a2V, wLor, dFwm, fshift, P, T, L, nA)
- On the fifth page, in the Python Package Check(Labtalk Script) edit box, enter
if(Python.chk("numpy") > 1)
return 1;
return 0;
if(Python.chk("numpy") > 1)
return 1;
return 0;
- On the sixth page, check Use Custom Code, and in Initialization Code box, enter
//Code to be executed to initialize parameters
//Get the current worksheet page.
range rpage=ry.getpage()$;
//Get the data worksheet
range rlayer=ry.getlayer()$;
//Get the data worksheet index
int inext=rlayer.index;
//Make sure the data workbook is active
win -a %(ry.getpage()$);
//Make sure the data worksheet is active
page.active=inext;
double Temp = mean(col(12));
T=Temp;
double Press = mean(col(13));
P=Press;
Vamp=0.99629;
a1V=2.31e-4;
wLor=8.95;
fshift=-2.54;
dFwm=1;
L=89.87071;
nA=1.95e-7*P/100*100;
- On the eighth page in Derived Parameters tab, set the values to coressponding parameters:
Unit = ug/m3
Names = ConcRef,wLorPval,fshiftPval
Meanings = Ref conc at T
In Derived Parameters Equations box, enter
ConcRef=(760/P)*((T)/293.15)*((nA/((10/1000)*8411821.73)*(1E+27/1000000))/(6.022140857E+23))*200.59*(100)^3*1000000
wLorPval=wLor*P/1000
fshiftPval=fshift*P/1000
- Click Finish button.
|