2.10.34 plotmatrix
Brief Information
Create a scatter matrix plot as embedded graphs in worksheet
X-Function Execution Options
Please refer to the page for additional option switches when accessing the x-function from script
Variables
Display
Name
|
Variable
Name
|
I/O
and
Type
|
Default
Value
|
Description
|
| Input
|
irng
|
Input
Range
|
<active>
|
Specify the input data range.
|
| Confidence Ellipse
|
ellipse
|
Input
int
|
1
|
Specify whether to add confidence ellipse for each graph based on the chosen confidence level.
|
| Confidence Level in %
|
conflevel
|
Input
double
|
95
|
This is only available when the ellipse variable is set to 1. Use it to specify the confidence level in percentage for the confidence ellipses. This value must be greater than 0 and less than 100
|
| Linear Fit
|
fit
|
Input
int
|
0
|
Specify whether to perform a linear fit to each pair of variables. When this is checked, the fitted line and the adjusted R^2 value will be added to each scatter graph.
|
| Exclude Missing Values Listwise
|
missing
|
Input
int
|
0
|
Specify whether to exclude missing values listwisely. That is, exclude the entire row for all datasets if there are any missing values in this row.
|
| Output Results
|
rd
|
Output
ReportData
|
[<input>]<new>
|
This determines where the calculated data for the ellipse and the fit are stored. The default location is a new worksheet within the source workbook.
|
| Result Graph
|
rt
|
Output
ReportTree
|
[<input>]<new template:=graph>
|
This determines where the graphs will be stored. The default location is a new worksheet based on the GRAPH.OTW template within the source workbook.
|
Description
This X-Function can be used to create a scatter matrix of multiple variables with normal distributions, which can be used to determine if pairs of such variables correlate or not.
Confidence ellipse can be added to each scatter plot. This helps you to judge the correlation of the pair of variables plotted in the graph.
Linear fit can be performed to each scatter plot. The inclination angle of the fitted line indicates the direction of the correlation. If it is positive, this means that the increase of one variable is likely to cause the increase of the other variable. While a negative angle indicates a reverse relationship. The slope of the fit varies from -1 (perfectly negative correlation) to +1 (perfect positive correlation).
Examples
// Create a Scatter Matrix using columns 2, 3 and 5 of the specified Worksheet
newbook na:=PlotMatrixEX op:=1;
wo -a 3; // Add 3 columns
col(1)=data(1,30);
col(2)=uniform(30);
col(3)=normal(30);
col(4)=uniform(30);
col(5)=col(3);
plotmatrix
irng:=[PlotMatrixEX]Sheet1!(2,3,5)
ellipse:=1
conflevel:=50
fit:=1;
// Here we create a new book with sheets for our data and our graphs.
// We then use this same book for gathering Scatter Matrix results
// for columns 1 and 2 in all sheets in our source book.
newbook na:=PMEx2 op:=1;
repeat 3 newsheet;
loop(ii,1,4) {
page.active = ii; // for each sheet
col(1) = uniform(25);
col(2) = uniform(25);
}
for( ii = 1 ; ii <= 4 ; ii++)
{
range rData = [PMEx2]$(ii)!(1,2);
plotmatrix
irng:=rData
ellipse:=1
conflevel:=50
fit:=1
rd:=[STATS]MyScatterData
rt:=[STATS]MyScatterGraphs;
}
Algorithm
Assuming the pair of two variables 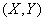 follows bivariate normal distribution, we can study the relationship of the two variables by this test. The confidence ellipse is centered at follows bivariate normal distribution, we can study the relationship of the two variables by this test. The confidence ellipse is centered at 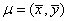 , and the major semiaxis , and the major semiaxis 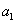 and major semiaxis and major semiaxis 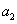 are given by the following equations: are given by the following equations:
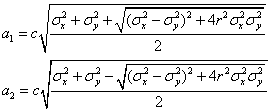
where 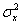 and and 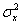 are the variances of are the variances of 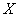 and and 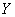 , , 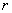 is the correlation coefficient of is the correlation coefficient of 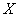 and and 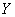 . .
For a given confidence level of 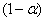 , the constant , the constant 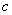 is: is:
1) Confidence ellipse for the population mean:
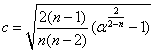
2) Confidence ellipse for prediction:
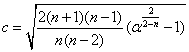
The inclination angle 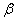 of the ellipse indicates the angle from the of the ellipse indicates the angle from the 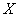 axis deasil. It is computed by the following equation: axis deasil. It is computed by the following equation:
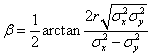
References
- 1. Lewlaw R. Paradowski.1997. Uncertainty Ellipses and Their Application to Interval Estimation of Emitter Position, IEEE Transactions on aerospace and electronic systems. 33. Page:126-133
- 2. J. Wesley Barnes. 2002. Statistical Analysis for Engineers and Scientists. Tsinghua University, China.
Related X-Functions
corrcoef
Keywords:confidence, ellipse, linear fit
|