2.4.8 fitpoly
Brief Information
Polynomial regression
Additional Information
Minimum Origin Version Required for all features: Origin 9.0
Command Line Usage
1. fitpoly iy:=(1,2) polyorder:=2 fixint:=0 intercept:=0 coef:=3 oy:=(4,5);
X-Function Execution Options
Please refer to the page for additional option switches when accessing the x-function from script
Variables
Display
Name
|
Variable
Name
|
I/O
and
Type
|
Default
Value
|
Description
|
| Input
|
iy
|
Input
XYRange
|
<active>
|
This variable specifies the input data range.
|
| Polynomial Order
|
polyorder
|
Input
int
|
2
|
This variable specifies the order of polynomial to be fit.
|
| Fix Intercept
|
fixint
|
Input
int
|
0
|
A value of 1 (checked in dialog) indicates fixed intercept.
|
| Fix Intercept At
|
intercept
|
Input
double
|
0
|
Specify the value of fixed intercept. If fixint is 0, this value is ignored.
|
| Polynomial Coefficients
|
coef
|
Output
vector
|
<optional>
|
This specifies the column or dataset variable to receive the polynomial coefficients, e.g. coef:=3, which means to output the polynomial coefficients to column 3.
|
| Output
|
oy
|
Output
XYRange
|
<optional>
|
This specifies the Output range to receive the polynomial fit curve.
|
| Number of Points
|
N
|
Output
int
|
<unassigned>
|
This specifies the variable to receive number of points in the fit.
|
| Adjusted residual sum of squares
|
AdjRSq
|
Output
double
|
<unassigned>
|
This specifies the variable to receive the adjusted coefficient of determination(R^2).
|
| Coefficient of determination (R^2)
|
RSqCOD
|
Output
double
|
<unassigned>
|
This specifies the column or dataset variable to receive the coefficient of determination((R^2).
|
| Polynomial Coefficients Errors
|
err
|
Output
vector
|
<optional>
|
This specifies the column or dataset variable to receive the polynomial coefficients standard errors
|
Description
Polynomial regression fits a given data set to the following model:
 . .
where 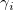 are the coefficients and are the coefficients and  is the error term. The error term represents the unexpected or unexplained variation in the dependent variable. It is assumed that the mean of the random variable is the error term. The error term represents the unexpected or unexplained variation in the dependent variable. It is assumed that the mean of the random variable  is equal to zero. is equal to zero.
Parameters are estimated using a weighted least-square method. This method minimizes the sum of the squares of the deviations between the theoretical curve and the experimental points for a range of independent variables. After fitting, the model can be evaluated using hypothesis tests and by plotting residuals.
It is worth noting that the higher order terms in polynomial equation have the greatest effect on the dependent variable. Consequently, models with high order terms (higher than 4) are extremely sensitive to the precision of coefficient values, where small differences in the coefficient values can result in a larges differences in the computed y value. We mention this because, by default, the polynomial fitting results are rounded to 5 decimal places. If you manually plug these reported worksheet values back into the fitted curve, the slight loss of precision that occurs in rounding will have a marked effect on the higher order terms, possibly leading you to conclude wrongly, that your model is faulty. If you wish to perform manual calculations using your best-fit parameter estimates, make sure that you use full-precision values, not rounded values. Note that while Origin may round reported values to 5 decimal places (or other), these values are only for display purposes. Origin always uses full precision (double(8)) in mathematical calculations unless you have specified otherwise. For more information, see Numbers in Origin.
Generally speaking, any continuous function can be fitted to a higher order polynomial model. However, higher order terms may not have much practical significance.
Examples
// This example shows how to use the fitpoly Polynomial Fit function and access the results.
// Get some sample data
newbook name:="Linear Regression Sample" sheet:=1 result:=ResultBook$;
impfile fname:=system.path.program$+"Samples\Curve Fitting\Multiple Gaussians.dat";
// Declare variables for coefficients and Adjusted R^2
dataset ds; // vector argument requires dataset
double MyR;
// Setup table for output
type Dataset\tA0\tA1\tA2\tA3\tAdjR^2;
separator 6;
// Now loop through all four curves, fit and report
loop(ii,2,5) {
fitpoly iy:=(1,$(ii)) polyorder:=3 coef:=ds AdjRSq:=MyR;
%N = wks.col$(ii).name$;
type %N\t$(ds[1],S*6)\t$(ds[2],S*6)\t$(ds[3],S*6)\t$(ds[4],S*6)\t$(MyR,S*6);
}
separator 6;
separator 6;
// Now loop through all four curves, fit and report
loop(ii,2,5) {
fitpoly iy:=(1,$(ii)) polyorder:=3 coef:=ds fixint:=1 intercept:=0 AdjRSq:=MyR;
%N = wks.col$(ii).name$;
type %N\t$(ds[1],S*6)\t$(ds[2],S*6)\t$(ds[3],S*6)\t$(ds[4],S*6)\t$(MyR,S*6);
}
Algorithm
Regression model:
For a given dataset (xi , yi ), i = 1,2,...n, where X is the independent variable and Y is the dependent variable, a polynomial regression fits data to a model of the following form:
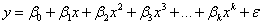
where k is the degree and, in Origin, it is a positive number that is less than 10. The error term  is assumed to be independent and normally distributed N(0, is assumed to be independent and normally distributed N(0, 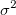 ). ).
To fit the model, assume that the residuals:
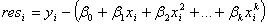
Are normally distributed with the mean equal to 0 and the variance equal to 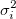 . Then the maximum likelihood estimates for the parameters . Then the maximum likelihood estimates for the parameters  can be obtained by minimizing the Chi-square, which is defined as: can be obtained by minimizing the Chi-square, which is defined as:
If the error is treated as weight, the Chi-square minimizing equation can be written as:
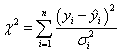
and:
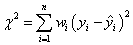
where  are the measurement errors. If they are unknown, they should all be set to 1. are the measurement errors. If they are unknown, they should all be set to 1.
Coefficient estimation by matrix calculation:
The calculation of the estimated coefficients is a procedure of matrix calculation. First, we can rewrite the regression model in the matrix form
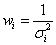
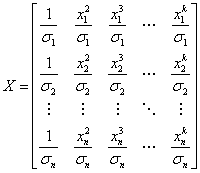
where:
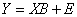
The estimate of the vector B is the solution to the linear equations, and can be expressed as:
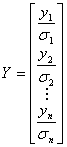  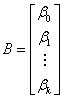 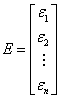
where 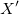 is the transpose of X. is the transpose of X.
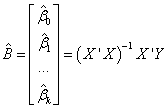
Inference in polynomial regression:
The ANOVA for the polynomial regression is summarized in the following table:
|
|
df
|
Sum of Squares
|
Mean Square
|
F Value
|
Prob> F
|
|
Model
|
k
|
SSreg = TSS - RSS
|
MSreg = SSreg / k
|
MSreg/ MSE
|
p-value
|
|
Error
|
n* - k
|
RSS
|
MSE = RSS / (n*-k)
|
|
|
|
Total
|
n*
|
TSS
|
|
|
|
(Note: If intercept is included in the model, n*=n-1. Otherwise, n*=n and the total sum of square is uncorrected.)
Where the total sum of square, TSS, is
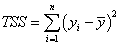 (for corrected model) (for corrected model)
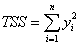 (for uncorrected model) (for uncorrected model)
And the residual sum of square (RSS) or sum of square error (SSE), which is actually the sum of the squares of the vertical deviations from each data point to the fitted line. It can be computed as:
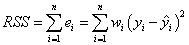
The result of the F-test is presented in the ANOVA table. The null hypothesis of the F test is that all of the partial coefficients are equal to zero, i.e.
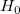 : : 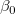 = = 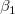 = = 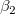 = ... = = ... = 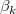 = 0 = 0
Thus, the alternative hypothesis is:
'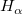 ': At least one ': At least one 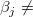 0 0
With the computed F-value, we can decide whether or not to reject the null hypothesis. Usually, for a given confidence level  , we can reject , we can reject 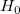 when F > when F > 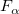 , or the significance of F (the computed p-value) is less than , or the significance of F (the computed p-value) is less than  . .
For the inference, we need to know the standard error of partial slopes, which may be computed as:
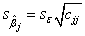
where  is the jth diagonal element of (X'X)-1. And is the jth diagonal element of (X'X)-1. And 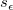 is the residual standard deviation (also called td dev, tandard error of estimate, or oot MSE) computed as: is the residual standard deviation (also called td dev, tandard error of estimate, or oot MSE) computed as:
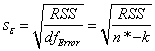
If the regression assumptions hold, we can perform the t-tests for the regression coefficients with the null hypotheses and the alternative hypotheses:
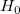 : :  = 0, = 0,
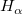 : : 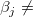 0, 0,
The t-value can be computed as:

With the t-values, we can decide whether or not to reject the null hypotheses. Usually, for a given confidence level  , we can reject , we can reject 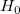 when |t| > when |t| > 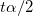 , or when the significant p-value less than , or when the significant p-value less than  . .
Confidence and Prediction interval:
For a particular value xp, the 100(1- )% confidence interval for the mean value of y at x=xp is: )% confidence interval for the mean value of y at x=xp is:
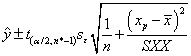
And the 100(1- )% prediction interval for the mean value of y at x=xp is: )% prediction interval for the mean value of y at x=xp is:
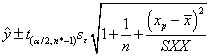
Coefficient of Determination:
The goodness of fit can be evaluated by coefficient of determination, R2, which is given by:
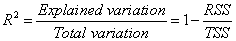
The adjusted R2 is used to adjust the R2 value for the degree of freedom. It can be computed as:
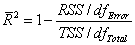
Then we can compute the R-value, which is simply the square root of R2:

Covariance and Correlation matrix:
The covariance matrix of the polynomial regression can be calculated as:
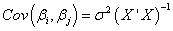
And the correlation between any two parameters is:

References
1. Bruce Bowerman, Richard T. O'Connell. 1997. Applied Statistics: Improving Business Processes. The McGraw-Hill Companies, Inc.
2. Sanford Weisberg. 2005. Applied Linear Regression, 2nd ed. John Wiley & Son, Inc., Hoboken, New Jersey.
3. William H. Press.; et al. 2002. Numerical Recipes in C++, 2nd ed. Cambridge University Press: New York.
Related X-Functions
fitLR, nlfit
Keywords:curve fitting
|