2.13.1.9 kstest
Brief Information
One sample Kolmogorov-Smirnov test for normality
Command Line Usage
kstest irng:=col(2)
X-Function Execution Options
Please refer to the page for additional option switches when accessing the x-function from script
Variables
Display
Name
|
Variable
Name
|
I/O
and
Type
|
Default
Value
|
Description
|
| Input
|
irng
|
Input
Range
|
<active>
|
Specify the input data range
|
| Statistics
|
stat
|
Output
double
|
<unassigned>
|
Specify the mean of the normal distribution. If value is <auto>, Origin will calculate it automatically
|
| Variance
|
df
|
Output
double
|
<unassigned>
|
Specify the variance of the normal distribution. If value is <auto>, Origin will calculate it automatically
|
| Statistics
|
prob
|
Output
double
|
<unassigned>
|
The computed test statistics, D.
|
Description
This function provides Kolmogorov-Smirnov test to compare the maximum distance between sample cumulative distribution function with the theoretical cumulative distribution function to determine whether the sample comes from a population of the theoretical distribution specified by user. Currently, Origin tests the normality only.
Examples
1. Highlight and right-click a column, select Fill Column With: Normal Random Numbers to fill some data on the column.
2. Type kstest on the command window. The probability of null hypothesis can be seen from kstest.prob.
Algorithm
For a given sample data 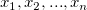 , let , let 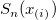 and and  ) represent the sample cumulative distribution function and the theoretical (null) cumulative distribution function respectively at the point ) represent the sample cumulative distribution function and the theoretical (null) cumulative distribution function respectively at the point 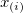 where where 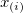 is the ith smallest sample observation, the K-S test provides a test of the null hypotheses is the ith smallest sample observation, the K-S test provides a test of the null hypotheses 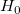 : The data are a random sample of observations from the theoretical distribution specified by user. Currently, Origin tests the normality only. : The data are a random sample of observations from the theoretical distribution specified by user. Currently, Origin tests the normality only.
To measure the difference between 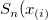 and and  , K-S test compute the maximum absolute difference between the two cumulative distribution functions: , K-S test compute the maximum absolute difference between the two cumulative distribution functions:

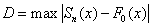
And then D will be used to compute the probability of null hypothesis.
Origin calls a NAG function, nag_1_sample_ks_test (g08cbc), to compute the statistics. Please refer to related NAG document, for more details on the algorithm.
References
William H. Press, etc. 2002. Numerical Recipes in C++. Cambridge University Press.
Related X-Functions
kstest2, swtest, lillietest
Keywords:variance
|