| Note: すべての関数は、 Origin 8 SR6 以降のバージョンでのみ利用できます。 |
| 名前 | 説明 |
|---|---|
| Between(str$, str1$, str2$)$ | str$のstr1$とstr2$の間の文字列または文字を抽出します。 サンプル:
|
| Char(number)$ | 1-255の整数をとり、ASCII文字を返します。 サンプル:
|
| Code(str$) | 文字列をとり、最初の文字のASCII文字を返します。例:
|
| Compare(str1$, str2$ [,Case]) | 2つの文字列をとり、一致した場合1、不一致の場合0を返します。 オプションCaseは、大文字と小文字の区別を制御し、1=真(デフォルト)、0=偽 です。 サンプル:
|
| CompareNoCase(str$, str2$) | 2つの文字列を取り、0 (同一)、-1(アルファベット順でstr$がstr2$より小さい)、または1(str$がstr2$より大きい)を返します。 サンプル:
|
| EnvVar(variableName$) | 文字列を取り、対応するWindows環境変数に格納されている文字列値を返します。この文字列が有効なWindows環境変数文字列でない場合、欠損値が返されます。 サンプル:
|
| Exact(str1$, str2$) | 2つの文字列をとり、大文字と小文字の区別を含めて一致した場合1、不一致の場合0を返します。例:
|
| Find(within$,find$[,StartPos]) | within$ でfind$を検索し、見つかった場合within$内の最初の文字の位置を返し、見つからなかった場合-1を返します。 オプションStartPosは、検索開始位置を制御します。(デフォルト=1)大文字小文字の区別あり。ワイルドカードは使用できません。 例:
|
| FindOneOf(within$,find$) | within$内で見つかった最初の文字をfind $で検索し、見つかった場合は、最初に見つかった文字の1ベースインデックスを返します。大文字小文字の区別あり。ワイルドカードは使用できません。 例:
|
| GetAt(str$,index) | str$のindexで指定された単一の文字を返します。例:
|
| GetFileExt(strFile$)$ | フルパスstrFile$からファイル拡張子を取得します。例:
|
| GetFileName(strFile$,bRemoveExt)$ | フルパスstrFile $からファイル名(bRemoveExt = 1の場合は拡張子なし)を取得します。例:
|
| GetFilePath(strFile$)$ | フルパスstrFile$からファイル拡張子を取得します。例:
|
| GetLength(str$) | str$の長さを取得します。例:
|
| GetToken(str$,n,chDelimiter)$ | トークンがchDelimiterで区切られているn番目のトークンを返します。例:
|
| IsEmpty(str$) | MS ExcelのISBLANK関数と同様です。ワークシートのセルが空かどうかを判断するために使用します。引数 str には、セルアドレスまたは値の列を指定できます。 例:
|
| IsFile(str$) | strが有効なフルパスファイル名の例であるかどうかをテストします。例:
|
| IsFormula(str$) | ワークシートのセルにセル数式が含まれているかどうかを確認します。 サンプル:
|
| IsPath(str$) | strが有効なファイルパスの例であるかどうかをテストします。例:
|
| Left(str$, n)$ | 文字列str$をとり、左から数えてn文字までを返します。 サンプル:
|
| Len(str$) | 文字列str$をとり、文字数を返します。例:
|
| Lower(str$)$ | 文字列str$をとり、小文字に変換します。例:
|
| MakeCSV(str$[, quote, output_delim, input_delim$])$ | 区切り文字を持つ文字列をとり、CSVに変換します。 出力を囲むためにオプションquoteを使用し、0(デフォルト)=囲み文字なし、1=一重引用符、2=二重引用符 を指定します。オプションoutput_delimは、 0=コンマ、1=セミコロン です。オプションinput_delim$は、ソース文字列の区切り文字を指定します。スペース区切りの場合は必要ありません。例:
|
| Match(within$,find$[,Case])
(2015 SR0) |
この関数は文字列find$とwithin$を比較し、内容が互いに一致するかを確認します。1(真、一致)または0(偽、不一致)を返します。文字列find$では"*" や "?" といったワイルドカードの使用をサポートしています。また、Caseで大文字と小文字の区別を制御します。0(デフォルト)=偽、1=真 です。例:
|
| MatchBegin(within$,find$[,StartPos,Case]) | 文字列within$を探し、find$の開始位置に応じた整数を返します。見つからない場合には-1を返します。 "*" や "?" といったワイルドカードの使用をサポートしています。オプションStartPosは、検索を始める文字の位置を指定します。デフォルトでは 1=最初の文字からの検索 です。オプションCaseは、大文字と小文字の区別を制御し、0=偽(デフォルト)、1=真 です。例:
|
| MatchEnd(within$, find$[, StartPos, Case]) | 文字列within$を探し、find$の終了位置に応じた整数を返します。見つからない場合には-1を返します。 "*" や "?" といったワイルドカードの使用をサポートしています。オプションStartPosは、検索を始める文字の位置を指定します。デフォルトでは 1=最初の文字からの検索 です。オプションCaseは、大文字と小文字の区別を制御し、0=偽(デフォルト)、1=真 です。例:
|
| Mid(str$, StartPos [, n])$ | 文字列str$をとり、StartPosからのn文字を返す、またはnが指定されていない場合にはStartPosから全てを返します。 サンプル:
|
| NumberValue(str$ [, Decimal$, Group$]) | 文字列または文字列のベクトルを受け取り、数値として返します。オプション Decimal は、文字列の10進区切り文字を解釈するために使用されます。オプション Group はグループ区切り文字を解釈するために使用されます。文字列とオプションは引用符で囲みます。 サンプル:
|
| Replace(within$, StartPos, n, replace$)$ | within$内のn文字をStartPosから始めて文字列replace$で置換します。 文字列replace$の長さはnと異なっていても問題ありません。例:
|
| Right(str$, n)$ | 文字列str$をとり、右から数えてn文字までを返します。 サンプル:
|
| Search(within$, find$[, StartPos]) | 文字列within$で、文字列find$を探し、位置を返します。ない場合には -1 を返します。 大文字と小文字の区別なし。ワイルドカード無効。オプションStartPosは検索開始位置を制御します。(デフォルト=1)例:
|
| SpanExcluding(source$, strEx$) | strExから文字が最初に出現する前のすべての文字を抽出して返します。大文字と小文字を区別します。例:
|
| SpanIncluding(source$, strIn$) | strInで識別される文字のセットに含まれる最初の文字から始めて、文字列ソースから文字を抽出します。大文字と小文字を区別します。例:
|
| Substitute(within$,sub$,find$ [, n])$ | within$内のfind$を探し、sub$で置き換えます。 オプションでn番目に見つかったものだけを置き換えます。例:
|
| Text(d[,fmt$])$
(9.1 SR0) |
double型を文字列に変換します。 オプションfmt$では出力をフォーマットしこれらの値をとります。指定されていない場合、列フォーマットを使用します。@SD桁を使用するために、空の文字列""を使用します。Origin全体の設定を使用するため、「*」を使用します。例:
|
| Token(str$,iToken[, iDelimiter])$ | 文字列str$をとり、インデックスiTokenに応じた部分文字列を返します。 オプションiDelimiterは区切り文字のASCII値で、0(デフォルト)=あらゆる空白、32=単一スペース、124= "|" です。"_" (ASCII 95), "|"(ASCII 124) などのほとんどの区切り文字をiDelimiterとして直接使用できます。例:
いくつかのシンボル文字は直接iDelimiterで使用できませんが、ASCII値はいつでも適用できます。 |
| Trim(str$[, n])$ | 文字列str$をとり、スペースを除きます。 パラメータnは、スペースをどのように取り除くかを制御し、0(デフォルト)=先行+後続、1=全て除く です。例:
|
| Upper(str$)$ | 文字列str$をとり、大文字で返します。 サンプル:
|
| Value(str$) | 文字列数str$をとり、double型として返します。 サンプル:
|
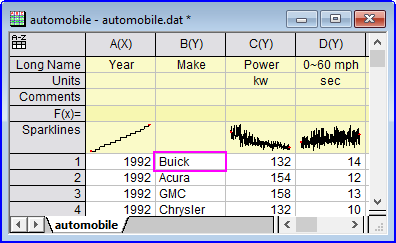
Note:文字列を操作するときに "$"を使用すると、混乱することがあります。

aa$=col(b)[1]; aa$=; // returns col(b)[1]
aa$=col(b)[1]$; aa$=; // returns Buick
aa$=upper(col(b)[1]$); aa$=; // returns upper(col(b)[1]$)
aa$=upper(col(b)[1]$)$; aa$=; // returns BUICK
| 名前 | 説明 |
|---|---|
| abs(x) | xの絶対値を返します。 サンプル:
|
| ceil(x[, sig])
(2019 SR0) |
指定した値xを0から離れた位置に調整し、xに最も近いsigの倍数に調整して値を返します。 サンプル:
|
| Combina(n,k)
(2019 SR0) |
与えられた n 要素から、k 要素選んだときの組み合わせの数を返します。 サンプル:
|
| Combine(n1,n2) | 与えられた n1 要素から、n2 要素を選んだ時の組み合わせの数を返します。 サンプル:
|
| Distance(px1, py1, px2, py2) | 2点のXY座標をとり、最短距離を返します。 サンプル:
|
| Distance3D(px1, py1, pz1, px2, py2, pz2) | 2点のXYZ座標をとり、3Dでの最短距離を返します。 サンプル:
|
| exp(x) | eのx乗を返します。 Note: x > 667 のときには欠損値を返します。例:
|
| expm1(x) | xの小さい値に対してexp(x)-1の値を正確に返します。 例:
|
| fact(n) | 非負の整数値の階乗を返します。 Note: n > 170 のときは欠損値を返します。Log_gamma関数を参照してください。例:
|
| factdouble(n) | 非負の整数値の二重階乗を返します。
n=奇数の場合、シーケンスは1*3*5...(n-2)*n、n=偶数の場合、シーケンスは2*4*6...(n-2)*n、n=0の場合、1として評価されます。n >299 の場合、欠損値を返します。例:
|
| floor(x[, sig])
(2019 SR0) |
与えられた値xを0に近づけ、xに最も近い有意数の倍数に調整して値を返します。 サンプル:
|
| gcd(n1, n2[, ...])
(2019 SR0) |
与えられた整数n1, n2, n3などのグループの最大公約数を返します。 例:
|
| frac(x) | double型の小数部分を返します。
サンプル:
|
| HaversineDistance(lon1,lat1,lon2,lat2,r[,degree])
(2017 SR0) |
半径r を持った球状にある2つのポイントの緯度経度を使うと、それらの大円距離を返します。オプションdegreeは緯度経度を単位として、度かラジアンのどちらを使うかを決定します。(デフォルトは度) サンプル:
|
| int(x) | double型のxを取り、切り捨て整数値を返します。 サンプル:
|
| ln(x) | xの自然対数を返します。 |
| ln1p(x) | xが1に非常に近いときのxの自然対数を返します。 |
| log(x) | xの底10のxの対数を返します。 |
| mod(n, m) | 整数nを整数mで割った時の整数の剰余(0に丸めた商)を返します。 サンプル:
|
| mod2(n,m) | 整数nを整数mで割った時の整数の剰余(負の無限大への丸めの商)を返します。係数の計算に使用される の商は の商は で丸められます。入力が負の場合、mod( で丸められます。入力が負の場合、mod( の商を0への丸めで計算)と異なる値を返します。サンプル: の商を0への丸めで計算)と異なる値を返します。サンプル:
|
| nint(x) | double型のxを取り、最近接整数に丸めます。 nint(x) 関数は round(x, 0) と同じ結果を返します。 |
| permut(n, k)
(2019 SR0) |
与えられたn要素の集合から、指定されたk要素の置換の数を返します。 サンプル:
|
| prec(x, n) | 値またはデータセットをとり、有効数字nで返します。 サンプル:
|
| product(vd) | vdのすべての数値を乗算し、積を返します。 サンプル:
|
| rmod(x, y) | Double型の値xをdouble型の値yで割った時のdouble型の値の剰余(0に丸めたsyouxをdouble型の値yで割った時のdouble型の値の剰余(0に丸めた商)を返します。  の商は の商は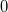 の丸めです。サンプル: の丸めです。サンプル:
|
| rmod2(x, y) | double型の値xをdouble型の値yで割った時のdouble型の値の剰余(負の無限大への丸めの商)を返します。  の商は の商は の丸めです。サンプル: の丸めです。サンプル:
|
| round(x, n) | 値またはデータセットをとり、小数点以下桁数nで返します。 Note: Origin 9.1 より新しい端数処理アルゴリズムを導入しています。システム変数@RNAは新旧メソッドを切り替えます。(旧メソッド@RNA=0、新メソッド@RNA=1(デフォルト))サンプル:
|
| sign(x) | 実数 x をとり、符号を返します。 X>0 の場合、1を返します。x<0 の場合、-1を返し、x=0 のとき、0を返します。 |
| sqrt(x) | double型のxを取り、平方根を返します。 |
| Derivative(vd[,n]) | ベクトル型 vd をとり、データリストの導関数を返します。 スムージングは無効です。オプションnで次数を指定します。(デフォルトは1です。) |
| DerivativeXY(vx, vy [, n]) | vxとvyの2つのベクトルを取り、曲線の導関数を返します。 オプションnで次数を指定します。(デフォルトは1です。) |
| Integral(integrand,lowerlimit,upperlimit[, arg1, arg2, ...]) | 1つの次元積分値を実行し、以下の積分値を返します。
|
| Integrate(vd) | 曲線下の面積積分を行います。 台形公式を使用します。 |
| IntegrateXY(vx, vy) | 曲線(vx,vy)下の面積積分を行います。 ベクトルvxは曲線のx座標を含み、vyはy座標を含みます。 |
| Interp(x,vX,vY[,method,bound,smooth,extrap])
(2015 SR0) |
x座標vxとy座標vyをとり、与えられた座標xにおいてy座標を補間/補外します。オプションmethod=0(線形、デフォルト)、1(3次スプライン)、2(3次Bスプライン)、3(Akima スプライン)method = 1のとき、bound は0 (自然) または 1 (not-a-knot)method=2 のとき、smooth=スムージング因子(負ではない)オプションextrapは、X値が参照範囲の外にあるときに適用されます。0(デフォルト)=最後の2点を使用してYを補外、1=全てのYを欠損値としてセット、2=最も近い入力XのY値を使用。 |
| permutationa(n, k)
(2019 SR0) |
与えられたn個の要素の集合から、指定されたk個の要素についての(反復を伴う)置換の数を返します。サンプル:
|
| 名前 | 説明 |
|---|---|
| beta(a, b) | パラメータaとbを持つベータ関数
|
| incbeta(x, a, b) | パラメータx,a,bを持つ不完全ベータ関数
|
| incf(x, m, n) | 不完全Fテーブル関数。 パラメータxは、積分範囲の上限、パラメータmは、分子分散の自由度、パラメータnは分母分散の自由度。 |
| incgamma(a,x) | パラメータaでxでの不完全ガンマ関数を計算。
ここで |
| inverf(x) | xでの逆誤差関数を計算 |
| j0(x) | 0次のベッセル関数 |
| j1(x) | 1次のベッセル関数 |
| jn(x, n) | n次のベッセル関数
ここで |
| y0(x) | 0次の第二種ベッセル関数 |
| y1(x) | 1次の第二種ベッセル関数 |
| yn(x, n) | n次の第二種ベッセル関数
ここで
|
| Note: 角度の単位(ラジアン、度、グラジアン)は、system.math.angularunits プロパティに依存します(メインメニューの環境設定:オプション:数値フォーマット) |
| 名前 | 説明 |
|---|---|
| acos(x) | xの逆余弦を返します。 x < -1 または x > 1 の場合、欠損値 ("--") を返します。 |
| acosh(x) | xの逆双曲線余弦の値を返します。 x < 1 の場合、欠損値 ("--") を返します。 |
| acot(x) | xの逆余接を返します。 入力xはどんな値でもとれます。第一または第二象限の値を返します。 |
| acoth(x) | |x| > 1 の逆双曲線余接の値を返します。 |
| acsc(x) | |x| の逆余割の値を返します。|x| < 1 の場合、欠損値("--")を返します。第一または第四象限の値を返します。 |
| acsch(x) | xの逆双曲線余割の値を返します。 x = 0 または x > ~3E153 の場合、欠損値("--")を返します。 |
| angle(x, y) | 原点(0,0)と座標(x,y)を結ぶ線と正のx軸の値の角度(ラジアン)を返します。 |
| Angleint1(px1, py1, px2, py2 [, unit, direction]) | 対のx,y座標をとり、2点とX軸によって定義される線間の角度を返します。 オプションunitは、0=ラジアン(デフォルト)、1=度 を制御し、オプションdirectionは0(デフォルト)は第一(+x,+y)と第四(+x.-y)象限に角度値を返し、1は0-2pi ラジアンまたは0-360度の値を返します。サンプル:
|
| Angleint2(px1, py1, px2, py2, px3, py3, px4, py4 [, unit, direction]) | (px1, py1)と(px2, py2)を結ぶ線と、(px3, py3)と(px4, py4)を結ぶ別の線の2つの線の間の角度を返します。 オプションunit=0(デフォルト)でラジアンを、unit=1で度を返します。オプションdirectionは返す値の方向を指定します。オプションdirection=0(デフォルト)の場合、第一象限(+x.+y)と第四象限(+x,-y)に制限、direction=1の場合、0-2pi ラジアンまたは0-360の値を返します。サンプル:
|
| asec(x) | xの逆正割を返します。 |x| < 1 の場合、欠損値("--")を返します。第一または第二象限の値を返します。 |
| asech(x) | xの逆双曲線正割の値を返します。0 < x ≤ 1 です。他のxの場合には欠損値("--")を返します。 |
| asin(x) | xの逆正弦を返します。-1 ≤ x ≤ 1 です。他のxの場合には欠損値("--")を返します。 |
| asinh(x) | x(実数)の逆双曲線正弦を返します。 |
| atan(x) | x(実数)の逆正接を返します。 |
| atan2(y,x) | 座標 x,y (double型) をとり、正のX軸と点(x,y) の間の角度を返します。atan(x) 関数の変化形です。-π と π の間の値を返します。角度は半時計回り方向(y>0)に対して正で、時計回り方向(y<0)に対して負となります。 |
| atanh(x) | xの逆双曲線正接の値を返します。-1 < x < 1 です。他のxの場合には欠損値("--")を返します。 |
| cos(x) | xの余弦を返します。 |
| cosh(x) | xの双曲線余弦の値を返します。 |
| cot(x) | xの余接を返します。 |
| coth(x) | xの双曲線余接の値を返します。 xは0ではない値です。おおよそ 絶対値 > 710 では、欠損値("--")を返します。 |
| csc(x) | xの余割を返します。 x = 0 の場合、欠損値("--")を返します。 |
| csch(x) | xの双曲線余割の値を返します。 xは0ではない値です。おおよそ x > 710 のときには欠損値("--")を返します。 |
| Degrees(angle) | ラジアンのangleをとり、度を返します。 |
| Radians(angle) | 度のangleをとり、ラジアンを返します。 |
| secant(x) | xの正割を返します。 Note:日付の秒の値を返すsec()関数と混同しないように注意してください。 |
| sech(x) | xの双曲線正割の値を返します。 おおよそ 絶対値 > 710 では、欠損値("--")を返します。 |
| sin(x) | xの正弦を返します。 |
| sinh(x) | xの双曲線正弦の値を返します。 |
| tan(x) | xの正接を返します。 |
| tanh(x) | xの双曲線正接の値を返します。 |
Note: Origin 2019以降 、Originには3つの日時システムがあります。古くからのデフォルトのシステムは、Originの日付と時間で説明されているように、調整済みのユリウス日システムです。次の例は、長期的なデフォルトの日時スキームに依存しており、 "Julian-date value"が表示されている場合、Originの調整日の値を参照します。これらの機能は、代替システムで動作するはずです...
date2str(today(), "MM/dd/yyyy")$ = 09/27/2018 // default date-time system, @DS=0 date2str(today(), "MM/dd/yyyy")$ = 09/27/2018 // "2018" system, @DS=2018
...ただし、カレンダーの日付と同じ数値は、システムによって異なります。
date(9/27/2018) = 2458388 // デフォルトの日付と時間システム date(9/27/2018) = 269 // 「2018」システム @DSP=2018
Originの代替日時スキームについては、Originの代替日時システムを参照してください。
| 名前 | 説明 |
|---|---|
| AddDay(vv)
(2021) |
時間ベクトルvvを取り、24時間後に時間が経過すると、追加された日データを返します。サンプル:
|
| Date(MM/dd/yyHH:mm:ss.##[,format$]) | 日付-時間の文字列をとり、ユリウス通日の値を返します。 format$が指定されていない場合、文字列はシステムのshort date フォーマットを使用して補間されます。format$文字列を指定せずに、1=デフォルト(MM/dd/yyyy),2(dd/MM/yyyy),3(yyyy/MM/dd) をとって最初の引数の日付フォーマットを制御します。サンプル:
|
| Date(yy,MM,dd) | 年として double型 yy、月として MM、日として dd をとり、ユリウス通日の値を返します。 サンプル:
|
| Date2str(d,format$)$ | ユリウス通日の値をとり、日付文字列を返します。 サンプル:
|
| DatePart(datepart$, d [, n])
(2016 SR1) |
ユリウス通に値(double型)dを取り、double型としてdatepart$で指定された一部日にちを返します。オプションnで週の始まりdatepart$=w または wwを指定します。 サンプル:
|
| Day(d[,n]) | ユリウス通日の値をとり、日数を返します。 オプションn=1 の場合、1から31(月)を返します。n=2のとき、1から366(年)を返します。例:
|
| Hour(d) | ユリウス通日の値をとり、整数として時間を返します。 0から23(0=12:00 A.M. , 23=11:00 P.M.)の値を返します。例:
|
| Minute(d) | ユリウス通日の値をとり、整数として時間を返します。(0から59) サンプル:
|
| Month(d) | ユリウス通日の値をとり、整数として月を返します。(0から12) サンプル:
|
| MonthName(d[,n])$ | ユリウス通日の値をとり、月名を返します。 月のフォーマットはオプションnで決まります。1=単一文字、3=3文字(デフォルト)、0=全て、-1=言語設定に関わらず英語の3文字です。例:
|
| Now() | 現在の日付/時刻を日付(ユリウス通日)の値として返します。 サンプル:
|
| Quarter(d) | ユリウス通日をとり、四半期を返します。 サンプル:
|
| Second(d[,n]) | ユリウス通日値または実数を受け取り、0 ~ 59.9999の範囲の実数として秒を返します。オプションn = 0は3桁以上の10進数字を表示しますが、ユリウス暦の日付の精度は4桁目の小数点以下を四捨五入すると0.0001秒に制限されます。 サンプル:
|
| Time(HH,mm,ss) と Time(HH:mm:ss[,Format$]) | Hh,mm,ss またはカスタム日付/時間文字列(HH:mm:ss=デフォルト)をとり、ユリウス通日の値を返します。オプションFormat$引数は、カスタム文字列フォーマットを指定します。サンプル:
|
| Time2str(d,format$)$ | ユリウス通日をとり、指定されたフォーマットの時間文字列を返します。 サンプル:
|
| Today() | 現在の日付をユリウス通日の値として返します。 |
| UnixTime(d1[, d2, n])
(2021) |
Unixタイムスタンプ値とユリウス日値の間で変換します。オプションのパラメータn = 0(デフォルト)の場合、d1(Unixタイムスタンプ)をユリウス日に変換します。 n = 1の場合、d1(ユリウス日)をUnixタイムスタンプに変換します。オプションのパラメータd2はタイムゾーンオフセットです。ユリウス日をUnixタイムスタンプに変換するときは、両方 のオプションのパラメーターを指定する必要があることに注意してください(オフセットがない場合、d2 = 0)。Unix タイムスタンプの単位は秒です。サンプル:
|
| WeekDay(d[,n]) | ユリウス通日をとり、曜日を返します。 オプションnは週の始まりと終わりの値を指定します。0(デフォルト)=日曜(0-6)、1=日曜(1-7)、2=月曜(0-6)、3=月曜(1-7)サンプル:
|
| WeekDayName(d[,n1,n2])$ | ユリウス通日(時間を含む)または、n2で定義された値をとり、平日を返します。 オプションn1は出力文字列の長さを制御します。-1=3文字を大文字表記、0=全てを表記し1文字目のみ大文字、1=1文字を大文字表記、3=3文字を表記し、1文字目のみ大文字。オプションn2で、週の開始と終了を指定します。0 = 0(日曜) - 6(土曜); 1 = 1(日曜) - 7 (土曜); 2 = 0(月曜) - 6(日曜); 3(デフォルト) = 1(月曜) - 7(土曜)。例:
|
| WeekNum(d[,n]) | ユリウス通日の値をとり、年を通した週数を返します。(1から53) 週の始まり(日曜か月曜)を定義するオプションがあります。例:
|
| Year(d) | ユリウス通日の値をとり、整数として年を返します。(0100から-9999) サンプル:
|
| YearName(d[,n])$ | ユリウス通日の値をとり、文字列として年を返します。 オプションnで文字列のフォーマットを指定し、0=2桁、1(デフォルト)=2桁(アポストロフィ付)、2=4桁 です。サンプル:
|
| 名前 | 説明 |
|---|---|
| if(con,val_true[,val_false])[$]
(2019 SR0) |
条件式conを評価し、比較がTRUEの場合はval_true、偽の場合はval_falseを返しますサンプル
|
| ifs(con1,val1[,con2,val2,]...[,con40,val40])[$]
(2019 SR0) |
複数の条件 con n を評価し、最初のTRUE条件の対応する d / str を返します。サンプル
|
| ifna(val,val_na)[$]
(2019 SR0) |
指定された数式valを計算し、結果がない場合は指定された文字列/数値val_naを返し、そうでない場合はvalの結果の文字列/数値表示を返します。サンプル
|
| switch(expression,val1,res1[,val2,res2]...[,val39,res39][,default])[$]
(2019 SR0) |
値のセットvalを使用して値式を評価し、一致する値valnがあれば、対応するresnを返します。サンプル
|
| 名前 | 説明 |
|---|---|
| fftamp(cx [,side])
(2015 SR1) |
複素ベクトルcx(通常FFTの複素結果)をとり、振幅を返します。オプションsideは、出力スペクトルを定義します(1=片側、2=両側とシフト)。サンプル:
|
| fftc(cx)
(2015 SR1) |
ベクトル型 cx をとり、複素FFT結果を返します。出力列のデータ型をcomplex(16)にする必要があります。 例:
|
| fftfreq(time, n[, side , shift])
(2015 SR1) |
サンプリング間隔timeと信号サイズnをとり、FFT結果の周波数を返します。オプションsideは、出力スペクトルを定義し(1=片側、2=両側)、shiftは両側のときにシフトするかを定義します。(0=シフトなし、1=シフト) サンプル:
|
| fftmag(cx [,side])
(2015 SR1) |
複素ベクトルcx(通常FFTの複素結果)をとり、マグニチュードを返します。オプションsideは、出力スペクトルを定義します。(1=片側、2=両側とシフト) サンプル:
|
| fftphase(cx[, side, unwrap, unit])
(2015 SR1) |
複素ベクトルcx(通常FFTの複素結果)をとり、位相を返します。オプションsideは、スペクトルの出力を定義(1=片側、2=両側とシフト)します。unwrapは位相角度の巻きの有無を(0=巻き、1=巻きなし)、unitは単位を定義します(0=ラジアン、1=度)。 サンプル:
|
| fftshift(cx)
(2015 SR1) |
複素ベクトルcx(通常FFTの複素結果または周波数)をとり、シフトされたベクトルを返します。出力列のデータ型をcomplex(16)にする必要があります。 サンプル:
|
| ifftshift(cx)
(2015 SR1) |
複素ベクトルcx(通常FFTの複素結果またはシフトされたFFT結果)をとり、シフトされていないベクトルを返します。出力列のデータ型をcomplex(16)にする必要があります。 サンプル:
|
| invfft(cx)
(2015 SR1) |
複素ベクトルcx(通常FFTの複素結果)をとり、逆FFT結果を返します。出力列のデータ型をcomplex(16)にする必要があります。 サンプル:
|
| windata(type, n)
(2015 SR1) |
type(ウィンドウ法)とn(ウィンドウサイズ)の整数をとり、サイズnのベクトルとしてウィンドウの信号を返します。サンプル:
|
| 名前 | 説明 |
|---|---|
| Count(vd[,n]) | ベクトル型 vd をとり、要素の数を返します。 オプションのnで要素を指定します。0 (デフォルト) = 全て; 1 = 数値; 2 = 欠損値 です。サンプル:
|
| Max(vd) | ベクトル型 vd をとり、最大値を返します。 サンプル:
|
| Mean(vd) | ベクトル型 vd をとり、平均を返します。 サンプル:
Note: 複数データセットの平均を行で計算する場合は、シンタックス
詳細は、sum(vd)関数を参照してください。 |
| Median(vd[,method]) | ベクトル型 vd をとり、中央値を返します。 オプションmethodで補間方法を指定します。0 (デフォルト) = 経験分布の平均; 1 = 近傍法; 2 = 経験分布; 3 = 加重平均右; 4 = 加重平均左; 5 = Tukey hinge です。サンプル:
|
| Min(vd) | ベクトル型 vd をとり、最小値を返します。 |
| Ss(vd [,ref]) | ベクトル型 vd をとり、平方和を返します。 平方和は、いくつかの参照値 ref を vd の各値から減算したあと計算されます。オプションrefはvdの平均をデフォルトとしますが、refは定数やデータセット、関数にすることもできます。例:
|
| StdDev(vd) | ベクトル型 vd をとり、標本標準偏差を返します。サンプル:
|
| StdDevP(vd) | ベクトル型 vd をとり、母標本標準偏差を返します。サンプル:
|
| Sem(vd)
(2020b) |
ベクトル型 vd をとり、標準誤差を返します。サンプル:
|
| Total(vd) | ベクトル型 vd をとり、要素の合計を返します。サンプル:
|
| averageif(vd, con$) | ベクトルvdと条件con$をとり、con$を満たす値の平均を返します。サンプル:
|
| Countif(vd,con$) | ベクトル型 vd をとり、条件 con$ を満たす値のカウントを返します。条件 con$ は二重引用符("")で囲む必要があります。
|
| Maxifs(vd,con$) | ベクトル型 vd をとり、条件 con を満たす最大値を返します。サンプル
|
| Minifs(vd,con$) | ベクトル型 vd をとり、条件 con を満たす最小値を返します。サンプル
|
| sumif(vd,con$) | ベクトル型 vd をとり、条件 con$ を満たす値の合計を返します。 |
| 名前 | 説明 |
|---|---|
| Correl(vx, vy) | データセットvxとvyをとり、相関係数を返します。サンプル:
|
| cov(vx, vy[, avex, avey]) | データセット vx と vy 、それぞれの平均 avex と avey をとり、 共分散を返します。 サンプル:
|
| Forecast(x,vx,vy) | x座標をvxとy座標でvyとし、線形回帰を実行して、与えられた座標xでy座標を計算または予測します。 |
| Intercept(vx,vy) | vx(独立)とvy(従属)の2つのベクトルを取り、線形回帰の切片を返します。 |
| mae(vobs,vpred)
(2023b) |
2つのベクトル、vobs(実測)とvpred(推測)をとり、平均絶対誤差を返します。 |
| mbe(vobs,vpred)
(2023b) |
2つのベクトル、vobs(実測)とvpred(推測)をとり、平均バイアス誤差を返します。 |
| rms(vd) | ベクトル型 vd をとり、二乗平均平方根返します。 |
| rmse(vobs,vpred)
(2023b) |
2つのベクトル、vobs(実測)とvpred(推測)をとり、二乗平均平方根誤差を返します。 |
| Slope(vx,vy) | vx(独立)とvy(従属)の2つのベクトルを取り、線形回帰の傾きを返します。 |
| ave(vd, size[, stats]) | ベクトルvdをとり、sizeの各グループの平均の範囲を返します。statsは、平均値でない他の統計値を出力するオプションを提供します。vdの要素がsizeの倍数でない場合、mod(vdSize,size)要素のみを平均した値を返します。サンプル:
|
| diff(vd[,n]) | ベクトルvdをとり、隣接要素間の相違の範囲を返します。返された範囲の最初の要素は vd(i+1)-vdiなどです。オプションのパラメータnの値に応じて、N-1、N、またはN + 1要素を返します。
|
| sum(vd) | Sum() 関数には2つのモードがあります。
「列」モードでは、単一列のベクトルvdを取り、累積和の値(1からi、i = 1、2、...、N)を保持するベクトルを返します。i+1番目の要素は最初のi要素の合計です。返される範囲の最後の要素は、データセット内のすべての要素の合計です。サンプル:
|
| Confidence(alpha, std, size[, dist]) | 有意水準 alpha、母標準偏差 std とサンプル size をとり、dist分布を使用した母平均の信頼区間を返します。サンプル:
|
| Geomean(vd) | ベクトル vd をとり、幾何平均を返します。
|
| Geosd(vd) | ベクトル vd をとり、幾何標準偏差を返します。
|
| Harmean(vd) | ベクトル vd をとり、調和平均を返します。
|
| histogram(vd, inc, min, max) | ベクトル vd、ビンの幅 = inc、vd の最小min と vdの最大 max をとり、データビンを生成します。各ビン上限上のポイントは次のビンに含まれます。 |
| Kurt(vd) | ベクトル型 vd をとり、尖度を返します。サンプル:
|
| lcl(vd[, level]) | ベクトル vdを取り、信頼水準levelでの下側信頼限界を返します。 サンプル:
|
| Mad(vd) | ベクトル型 vd をとり、平均絶対偏差を返します。 サンプル:
|
| Mode(vd) | ベクトル型vdをとり、vd内で最も頻度の高い数を返します。例:
|
| Modes(vd) | ベクトル型vdをとり、vd内で最も頻度の高い数のベクトルを返します。例:
|
| Percentile(vx, vy) | ベクトル型vxをとり、vyで指定された各値のパーセンタイル値を返します。 サンプル:
|
| QCD2(n) | サンプルサイズ n をとり、品質管理D2係数を返します。サンプル:
|
| QCD3(n) | サンプルサイズ n をとり、品質管理D3係数を返します。係数D3は、X-R管理図における3シグマ下部管理限界です。サンプル:
|
| QCD4(n) | サンプルサイズ n をとり、品質管理D4係数を返します。係数D4は、X-R管理図における3シグマ上部管理限界です。サンプル:
|
| Skew(vd) | ベクトル型 vd をとり、歪度を返します。サンプル:
|
| ucl(vd[, level]) | ベクトル vdを取り、信頼水準level(デフォルトは0.95)での上側信頼限界を返します。サンプル:
|
| Emovavg(vd,n[,method]) | ベクトル型vd、整数 n = 時間幅をとり、指数移動平均を返します。オプションmethodで計算の開始位置を指定します。0 (デフォルト) = ポイントnから; 1 = ポイント1から。サンプル:
|
| Mmovavg(vd,n) | ベクトル型vd、整数 n = 時間幅をとり、修正移動平均を返します。サンプル:
|
| Movavg(vd,back,forward[,missing]) | ベクトルvd をとり調整した範囲[i-back, i+forward]の、i ポイントの移動平均を返します(i は現在の行番号)。オプションmissingで、欠損値を省略するか決定します。サンプル:
|
| Movcoef(v1,v2,back,forward[,missing]) | ベクトルv1 および v2をとり調整した範囲[i-back, i+forward]の、i ポイントの移動相関係数のベクトルを返します(i は現在の行番号)。オプションmissingで、欠損値を省略するか決定します。サンプル:
|
| Movrms(vd,back[,forward]) | ベクトルvd をとり調整した範囲[i-back, i+forward]の、i ポイントの二乗平均平方根を返します(i は現在の行番号)。 サンプル:
|
| Movslope(vx,vy[,n]) | vx(独立)とvy(従属)の2つのベクトルを取り、各ポイントの移動傾きのベクトルを返します。オプション n はウィンドウ幅を指定します(>1)。nが偶数の場合、1を加えます。n を指定しない場合、入力の線形フィットの傾きの値を返します。サンプル:
|
| Tmovavg(vd,n[,missing]) | ベクトル型vd、整数 n = 時間幅をとり、三角移動平均を返します。オプションmissingで、欠損値を省略するか決定します。サンプル:
|
| Wmovavg(vd,vw) | ベクトル型 vd (スムージングのためのデータ)、vw (インデックスされた重み付き因子)をとり、加重移動平均のベクトルを返します。サンプル:
|
| 名前 | 説明 |
|---|---|
| betacdf(x,a,b[,tail]) | パラメータ aと bを持つ xにおけるベータ累積分布関数を計算します。aとbはすべて正でなければならず、xは区間[0,1]上になければなりません。tailは返される確率が下側のtailまたはupper tailであることを決定します。 |
| binocdf(k,n,p) | 二項分布で、n, p.に対応するパラメータを使って、与えられた値kでの上側確率/下側確率および点確率を計算します。
|
| bivarnormcdf(x,y,corre) | 二変量正規分布の下側確率を計算します。
|
| chi2cdf(x,df[,tail]) | 自由度df を持つカイ二乗分布に対する下側確率を計算します。 |
| foldnormcdf(x,mu,sigma) | 折り畳まれた正規分布の下側確率を計算します。 |
| fcdf(f,ndf,fdf[,tail]) | f における分子ndf と分母の変数fdfの自由度の変数F累積分布関数を計算します。tailは返される確率が下側のtailまたはupper tailであることを決定します。 |
| gamcdf(g,a,b[,tail]) | 形状パラメータa とスケールパラメータ bを使用し、ガンマ変量g の自由度を持つガンマ分布の下側確率を計算します。tailは返される確率が下側のtailまたはupper tailであることを決定します。 |
| hygecdf(k,m,n,l) | 対応するパラメータを使った超幾何分布で、与えられた値での下側確率を計算します。
ここで、n は母集団のサイズ、m は母集団の中で成功状態の数、l は引き分けのサンプル数です。 |
| landaucdf(x,mu,sigma[,tail])
(2024b) |
位置パラメータmuとスケールパラメータsigmaを使用して、xにおけるランダウ分布の累積密度関数を計算します。 tailは、返される確率が下側か上側であるかを決定します。 |
| logncdf(x,mu,sigma[,tail])
(2015 SR0) |
対応するパラメータmuおよびsigmaを使用してLognormal分布に関連付けられた、指定された値xの指定されたtail型テールの確率を計算します。tailが指定されていない場合、低いテール確率が返されます。tailが指定されていない場合、低いテール確率が返されます。 |
| ncbetacdf(x,a,b,lambda) | 非心ベータ分布の下裾で累積分布関数を計算します。
|
| ncchi2cdf(x,f,lambda) | 非心カイ二乗分布の下側確率を計算します。
|
| ncfcdf(f,df1,df2,lambda) | 非心ディガンマまたは分散比分布の下側確率を計算します。
ここで
なお、 |
| nctcdf(t,df,delta[,maxiter]) | 非心のスチューデントt分布に対する下側確率を計算します。
|
| normcdf(x[,tail]) | 正規の累積分布に関連付けられた、指定された値xxの指定されたtail型テールの確率を計算します。 |
| poisscdf(k,lambda) | ポアソン分布で、lambda に対応するパラメータを使って、与えられた値 k での下側確率を計算します。
|
| srangecdf(q,v,group) | スチューデント範囲統計分布の下側の裾に関連付けられた確率を計算します。
ここで
|
| tcdf(t,df[,tail]) | スチューデントt分布の累積分布関数に自由度dfを用いて指定されたtail型テールの確率を計算します。 |
| wblcdf(x,a,b) | パラメータaとbを使って、x値に対する下側ワイブル累積分布関数を計算します。
ここで、 |
| 名前 | 説明 |
|---|---|
| betapdf(x,a,b) | パラメータ a と bを持つベータ分布の確率密度関数を返します。
|
| binopdf(x,nt,p)
(2015 SR0) |
パラメータ nt と pを持つ二項分布の確率密度関数を返します。
ここで、 |
| cauchypdf(x,a,b)
(8.6 SR0) |
コーシー確率密度関数 (別名ローレンツ分布)
|
| exppdf(x,lambda)
(8.6 SR0) |
Xの値で評価される速度パラメータλを持つ指数分布の確率密度関数を返します。
|
| foldnormpdf(x,mu,sigma) | 平均 mu と標準偏差 sigma の折りたたまれた正規分布を使用して、Xの各値における確率密度関数を計算します。
|
| gampdf(x,a,b)
(8.6 SR0) |
パラメータa およびb を持つガンマ確率密度を返します。
ガンマ分布のデータセットからスケールと形状パラメータのa とb を生成するには、推定関数gamfitを使用します。 |
| ks2d(vx, vy[,bandwidth, grid, interp, binned])
(2020) |
指定された帯域幅法と密度法を使用して、ポイント (x, y) での2Dカーネル密度を返します。ここでvxはX座標値のベクトル、vyはY座標値のベクトルです。帯域幅法、グリッド(帯域幅法のみ)、補間、密度のオプション(interp = 1(true)の場合のみ適用可能)。
ここでn はベクトルvx または vyの要素の数で、インデックスi はベクトルvx またはvy のi番目の要素、最適スケール(wx, wy)は推定関数kernel2widthで推定されます。 |
| ks2density(x,y,vx,vy,wx,wy)
(2015 SR0) |
スケール(wx, wy)のデータセット (vx, vy)で確率される関数で(x, y)での2Dカーネル密度を返します
ここでn はベクトルvx または vyの要素の数で、インデックスi はベクトルvx またはvy のi番目の要素、最適スケール(wx, wy)は推定関数kernel2widthで推定されます。 |
| ksdensity(x,vx,w)
(2015 SR0) |
バンド幅wのベクトルvxのxにおけるカーネル密度を返します。
ここで、n はベクトルvXのサイズ、K はカーネル関数で、Originは通常 (ガウス) カーネル関数 |
| landaupdf(x,mu,sigma)
(2024b) |
位置パラメータ mu とスケール パラメータ sigma をもつランダウ分布を使用して、x の各値における確率密度関数を計算します。 |
| lappdf(x,mu,b)
(8.6 SR0) |
ラプラス確率密度関数 |
| lognpdf(x,mu,sigma)
(8.6 SR0) |
分布パラメータmu とsigma を持つ対数正規確率密度関数のXでの値を返します。
|
| normpdf(x,mu,sigma)
(8.6 SR0) |
平均 mu と標準偏差 sigma の正規分布を使用して、Xの各値における確率密度関数を計算します。
|
| poisspdf(x,lambda)
(8.6 SR0) |
lambdaでの平均値パラメータを使って、Xの各値のポアソン確率密度関数を計算します。
|
| wblpdf(x,a,b)
(8.6 SR0) |
パラメータ a と bを持つワイブル分布の確率密度関数を返します。
ワイブル分布のデータセットからスケールと形状パラメータのa とb を生成するには、推定関数wblfitを使用します。 |
| 名前 | 説明 |
|---|---|
| betainv(p,a,b) | 指定したベータ分布の逆累積分布関数を返します。 |
| chi2inv(p,df) | nu で指定されたパラメータを持つXでの対応する確率に対するカイ二乗累積密度関数の逆数を計算します。
|
| finv(p,df1,df2) | パラメータdf1 とdf2 を持つp におけるF 累積密度関数を計算します。
ここで、 |
| foldnorminv(p,mu,sigma) | 分布パラメータmuとsigmaを持つ折りたたまれた正規分布の指定された下側確率pに関連する偏差xを計算します。 |
| gaminv(p,a,b) | パラメータaとb を持つpにおけるガンマ累積密度関数を計算します。
ここで |
| Landauinv(p,mu,sigma)
(2024b) |
位置パラメータmuおよびスケールパラメータsigmaを使用して、pにおけるランダウ累積密度関数の逆関数を計算します。 |
| logninv(p,mu,sigma)
(2015 SR0) |
パラメータmu と sigma の対数正規分布の下側確率pに関連づいた偏差xを計算します。
ここで、 |
| norminv(p) | 標準正規分布の与えられた下側確率pでの偏差xを計算します。
ここで |
| srangeinv(p,v,ir) | スチューデント範囲統計分布の下側確率での偏り xを計算します。
|
| tinv(p,df) | 自由度を持つスチューデントt分布の下側確率の偏りを計算します。
|
| wblinv(p,a,b) | パラメータ a と b を使って、与えられた確率に対する逆ワイブル累積分布関数を計算します。
|
このカテゴリーの関数のうち、 rnd()/ran()およびgrnd()は、1つの値を返します。他の関数は範囲を返します。
| Note:乱数生成のOriginのメソッドのシードアルゴリズムは、バージョン2016で変更されました。詳細は、システム変数@ranを参照してください。 |
| 名前 | 説明 |
|---|---|
| Data(x1,x2,inc) | x1 と x2 の2つの値でデータセットを作ります。x1 から x2 の範囲で、増分は inc です。x1 = x2の場合、x1の値でのinc数を返します。incのデフォルト値は1です。サンプル:col(A) = data(0,100,5) は、列Aを0から100、増分5の値を入力します。
|
| grnd() | 関数grnd()は、平均=0と標準偏差=1を持つ、正規(ガウス)分布の乱数の標本値を返します。初期値と値のシーケンスは、各Originセッションで同じです。引数は必要ありません。一般に、この関数は、式 grnd()*sd+m を使用して、既知の平均値と標準偏差の正規分布からランダムな値を返すために使用されます。サンプル:
|
| normal(npts[,seed]) | nptsの範囲を返します。値は、平均=0、標準偏差=1の正規(ガウス)分布で与えられる正規乱数です。seedが省かれている場合には、この関数が使われる度に異なるseedが使われます。平均値と標準偏差を指定して、正規分布のランダム値を列に入力するために使用できます: normal(npts)*sd+m。サンプル:
|
| pattern(vd, onerepeat, seqrepeat) および pattern(x1,x2,inc,onerepeat,seqrepeat) | パターン化数値またはテキストデータを返します。pattern(vd, onerepeat, seqrepeat)は、文字列シリーズ vd と vd にあるそれぞれの要素を Onerepeat かつ、文字列全体を onerepeat 回繰り返します。pattern(x1,x2,inc,onerepeat,seqrepeat) は、増分incで増加するx1 から x2 の範囲でデータセットを生成します。データセットの個々の要素は、onerepeat回繰り返され、データセット全体はseqrepeat回繰り返されます。文字列シリーズの要素は、パイプ (|)、カンマ(,)、またはスペースや、 範囲変数によって分割されます。サンプル:
|
| Poisson(n, mean [,seed]) | 平均値 mean のポアソン分布を持つn個のランダムな整数を返します。 seed は任意で乱数生成のシードを提供します。サンプル:
|
| ran([seed]) および rnd([seed]) | 一様分布の標本から0から1の間の値を返します。オプションseedが正の場合、0を返します。seed ≤ 0 あるいは、引数がない場合は、乱数系列中の次の数を返します。 |
| uniform(npts [,seed]) および uniform(npts, vd) | nptsの範囲を返します。オプション seed は値、データ範囲、区切り文字列 ("|", "," またはスペース) 、文字列配列です。seed が値の場合、一様乱数を返します。seed がデータ範囲、文字列配列の場合、データ範囲や文字列から選ばれた値が返されます。seedが省かれている場合には、この関数が使われる度に異なるseedが使われます。この関数も、引数として、ベクトル vd を受け入れます。 |
| 名前 | 説明 |
|---|---|
| Category(vd)$
(2020b) |
カテゴリデータのベクトルvdを取り、すべてのカテゴリをワークシートの列に返します。カテゴリ順はソース列に従います。サンプル:
|
| Catindex(vd)
(2020b) |
カテゴリデータのベクトルvdを取り、各要素のカテゴリインデックスをワークシート列に返します。サンプル:
|
| Catrows(vd[,option])
(2024b) |
カテゴリデータのベクトルvdを取り、カテゴリごとのすべての行インデックスのパイプ区切りリストを返します。オプションの option で、各カテゴリのすべて/最初/最後のインデックスを返すかどうかを決定します。カテゴリ順はソース列に従います。サンプル:
|
| Cattext(n,vd)$
(2020b) |
カテゴリデータのベクトルvdを取り、n番目のカテゴリ値を返します。サンプル:
|
| Findmasks(vd) | マスクされたデータを含む vd をとり、マスクされたポイントのインデックスからなるベクトルを返します。 サンプル:
|
| Firstpoint(vd) | ベクトル型 vd をとり、データセットvdの最初の値を返します。 サンプル:
|
| Idx(vBool) | 単一のベクトルを含む条件式vBoolを評価し、条件を満たすすべてのレコードの行インデックスを含む整数のベクトルを返します。サンプル:
|
| Index(d,vd[,n]) | 単調なデータのベクトル vd をとり、データポイントdの番号を返します。オプションn = 0 (デフォルト)はdの値と同じ、または近い値を見つけ、 n = 1 は ≤ d、n = 2 は ≥ dを探します。vd が狭義単調でなくテキストも含まない場合は、-2を返します。サンプル:
|
| Lastpoint(vd) | ベクトル型 vd をとり、最大値を返し、データセットvdの最初の値を返します。 サンプル:
|
| List(val,vd) | ベクトル vd をとり、値val が最初のに出現したデータセットインデックス番号を返します。valがない場合、0を返します。サンプル:
|
| lookup(str$,vs,vref[,option,Case])[$]
(2015 SR0) |
ベクトルvs内で、文字列str$を検索し、同じインデックスのベクトルvref(数値または文字列)の値を返します。optionにより一致の精度を決めます。Case = 0(デフォルト)の場合、大文字小文字の区別をしません。サンプル:
|
| table(vd,vref,d[,option])[$]
(2015 SR0) |
ベクトルvd内の値dを検索し、同じインデックス番号を持つvref内の値を返します。vrefに応じて数値か文字列を返します。パラメータoptionはパラメータdの検索を修正します。-1(デフォルト) = vd vs vrefで線形補間を実行し、補間された値を返す; 0 = ≤ d の直近の値を検索; 1 = ≥ d の直近の値を検索; 2 = 値に等しいまたは直近の値を検索 |
| unique(vs[, sort, occurrence, sort2])
(2018b) |
ベクトル型 vs をとり、固有値を返します。パラメータsortは、返された固有値を並べ替えるかどうかを決定します。1(既定)= sort ascendingly; 0 =ソートなし; 2 =降順に並べ替えます。パラメーターoccurrenceは、重複した値を減らす方法を指定します。0 (デフォルト) = 最初の重複値を保持、1 = 最後の重複値を保持。sort2は、出現の処理方法を決定します: 0 (デフォルト) = 出現をソートしない、1 = 出現を昇順でソートします。2 =出現を降順にソートします。例:
|
| ReportCell(sBook$,sSheet$,sTable$,sRowRef$,sColRef$)
(2021b) |
指定されたブック名sBook、シート名sSheet、テーブル名sTable、およびセルの行と列の参照sRowRefとsColRefによるレポートシートテーブルセルへアクセスします。サンプル: Book1データでガウスフィット後、以下の式
Note:この関数は、セルの式でのみ使用できます。 |
| Xindex(x,vd[,option]) | ベクトル vd (Yデータセット)をとり、x 値に近い vd のXデータセット内の値のインデックス番号を返します。どのインデックスを返すか、optionで指定します。0 (デフォルト) = 左から等しいか最も近い; 1 = 右から等しいか最も近い; 2 = 左右から等しいか最も近い。必要条件:(1) vd はY列である; (2) vd の名前は実際のYデータセットと一致; (3) Xデータセットは昇順。サンプル:
|
| Xvalue(n,vd) | ベクトルvd (Y またはZデータセット)をとり、行番号 n に対応するX値を返します。サンプル:
|
| Errof(vd) | ベクトル vd(データセット)をとり、vdの誤差値を含むデータセット(xEr/yEr)を返します。サンプル:
|
| hasx(vd) | データセットvd を取り、vdがアクティブレイヤのXデータセットに対してプロットされている場合、1を返します。そうでなければ、0を返します。サンプル:
|
| IsMasked(n,vd) | ベクトル型 vd をとり、n = 0 の場合はマスクされたポイント数を返します。n = データポイントのインデックス番号の場合、それがマスクされていれば1、されていなければ0を返します。サンプル:
|
| Xof(vd) | Xデータセットに関連するYデータセットのベクトル名 vd をとり、Xデータセットの名前を含む文字列を返します。サンプル:
|
| 名前 | 説明 |
|---|---|
| asc(str$) | 入力文字列をとり、文字列の最初の文字に対応するASCII コード(十進法)を返します。この関数はcode関数と処理をします。サンプル:
|
| corr(vx,vy,k[, n]) | 2つのデータセット vx と vy、ラグサイズ k をとり、2つのデータセット間の相関を返します。オプション n は、ポイントの数です。ラグパラメータ k は、スカラーまたはベクトルです。kがベクトルの場合、関数はベクトルを返し、スカラーの場合はスカラーを返します。サンプル:
|
| dropNA(vd[, text]) | ベクトル型 vdをとり、欠損値とマスク値を削除します。オプションパラメータtextでテキストの扱いを指定します。 サンプル:
|
| join(rA, rB, ...) | rA1:rA2, rB1:rB2,... として示される2つ以上の範囲を取り、それらを1つのデータセットに結合します。サンプル:
|
| peaks(vd, width, minht) | ベクトルvdをとり、width とminhtを使用して検索されたピークのインデックスのデータセットを返します。width は、テストポイントの両側のポイント数です。minht はY軸の単位です。インデックスiで表されるピークは、(i-width)又は(i+width)のデータ値より大きいminhtとなります。サンプル:
|
| rank(vd[, n]) | データセットvdをとってソートし、ランク付けされたインデックスを返します。n = 0 (デフォルト)の場合、vdは昇順でソートされ、n = 1の場合降順でソートされます。vdに重複した値が存在する場合、重複した各値のランク付けされたインデックスの平均数を返します。サンプル:
|
| reverse(vd) | ベクトル vd をとり順序を反転します。 サンプル:
|
| sort(vd) | データセットをとり、昇順でソートして返します。サンプル:
|
| treplace(vd,val1,val2[, cnd]) | 条件cndが合致すると、データセットを他の値と入れ替えます。データセット vd をとり、各値を cnd に対してval1 と比べ、比較が真の場合 val2 (または -val2) で置き換えます。偽の場合は値を残すか欠損値("--")で埋めます。 |
| 名前 | 説明 |
|---|---|
| airy_ai(x) | Airy 関数Ai(x)の近似を評価します。 |
| airy_ai_deriv(x) | Airy 関数Ai(x)の微分の近似を評価します。 |
| airy_bi(x) | Airy 関数Bi(x)の近似を評価します。 |
| airy_bi_deriv(x) | Airy 関数Bi(x)の微分の近似を評価します。 |
| 名前 | 説明 |
|---|---|
| bessel_i0(x) | Bessel i0。第一種修正ベッセル関数の近似値 I0(x)を求めます。 |
| bessel_i0_scaled(x) | Bessel i0 scaled。式 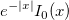 の近似値を求めます。 の近似値を求めます。
|
| bessel_i1(x) | Bessel i1。第一種修正ベッセル関数 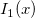 の近似値を求めます。 の近似値を求めます。
|
| bessel_k1_scaled(x) | Bessel i1 scaled。式 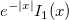 の近似値を求めます。 の近似値を求めます。
|
| bessel_i_nu(x,nu) | Bessel i nu。第一種修正ベッセル関数の近似値 I /4 (x) を求めます。 /4 (x) を求めます。
|
| bessel_i_nu_scaled(x,nu) | スケール済みBessel i nu。第一種修正ベッセル関数 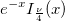 の近似値を求めます。 の近似値を求めます。
|
| bessel_j0(x) | Bessel j0。第一種ベッセル関数 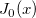 を計算します。 を計算します。
|
| bessel_j1(x) | Bessel j1。第一種ベッセル関数 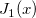 の近似値を求めます。 の近似値を求めます。
|
| bessel_k0(x) | Bessel k0。第二種修正ベッセル関数,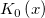 の近似値を求めます。 の近似値を求めます。
|
| bessel_k0_scaled(x) | Bessel k0 scaled。式 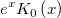 の近似値を求めます。 の近似値を求めます。
|
| Bessel_k1(x) | Bessel k1。第二種修正ベッセル関数,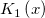 の近似値を求めます。 の近似値を求めます。
|
| bessel_k1_scaled(x) | Bessel k1 scaled。式 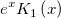 の近似値を求めます。 の近似値を求めます。
|
| bessel_k_nu(x,nu) | Bessel k nu。第二種修正ベッセル関数,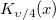 の近似値を求めます。 の近似値を求めます。
|
| bessel_k_nu_scaled(x,nu) | スケール済みBessel k nu。第二種修正ベッセル関数,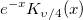 の近似値を求めます。 の近似値を求めます。
|
| bessel_y0(x) | Bessel y0。第二種ベッセル関数 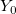 ,x > 0を計算します。近似値はChebyshev拡張に基づいています。 ,x > 0を計算します。近似値はChebyshev拡張に基づいています。
|
| bessel_y1(x) | Bessel y1。第二種ベッセル関数 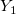 ,x > 0を計算します。近似値はChebyshev拡張に基づいています。 ,x > 0を計算します。近似値はChebyshev拡張に基づいています。
|
| 名前 | 説明 |
|---|---|
| erf(x) | 誤差関数(または正規誤差積分) |
| erfc(x) | 誤差関数の補数に対する近似値を計算します。 |
| erfcinv(dy) | 指定したyの逆相補誤差関数の値を計算します。 |
| erfcx(x) | スケーリング相補誤差関数 |
| erfi(c) | 複素数または実数を取り、虚数誤差関数を返します。 |
| erfinv(dy) | 逆誤差関数 |
| 名前 | 説明 |
|---|---|
| gamma(x) | ガンマ関数。式 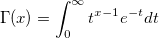 を計算します。 を計算します。
|
| incomplete_gamma(a,x) | 不完全ガンマ関数 |
| log_gamma(x) | 対数ガンマ関数。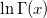 を計算。x > 0。 を計算。x > 0。
|
| real_polygamma(x,k) | ポリガンマ関数。Psi関数 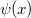 のk 次導関数の近似を計算します。 のk 次導関数の近似を計算します。
|
| 名前 | 説明 |
|---|---|
| cos_integral(x) | NAG 余弦積分関数。式  を計算します。 を計算します。
|
| cumul_normal(x) | 累積正規分布関数を計算します。 |
| cumul_normal_complem(x) | 累積正規分布関数の補数に対する近似値を計算します。 |
| elliptic_integral_rc(x,y) | 一種のNAG楕円積分。積分 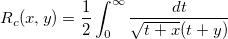 の近似値を計算します。 の近似値を計算します。
|
| elliptic_integral_rd(x,y,z) | 二種のNAG対称楕円積分。積分 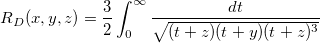 の近似値を計算します。 の近似値を計算します。
|
| elliptic_integral_rf(x,y,z) | 一種のNAG対称楕円積分。積分 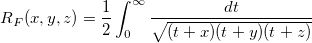 の近似を計算します。 の近似を計算します。
|
| elliptic_integral_rj(x,y,z,r) | 三種のNAG対称楕円積分。積分 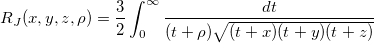 の近似を計算します。 の近似を計算します。
|
| exp_integral(x) | NAG 指数積分関数。式 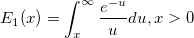 を計算します。 を計算します。
|
| fresnel_c(x) | NAGフレネル積分関数C。フレネル積分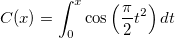 の近似を計算します。 の近似を計算します。
|
| fresnel_s(x) | NAGフレネル積分関数S。フレネル積分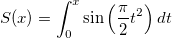 の近似を計算します。 の近似を計算します。
|
| sin_integral(x) | NAG 正弦積分関数。式 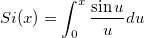 を計算します。 を計算します。
|
| 名前 | 説明 |
|---|---|
| kelvin_bei(x) | ケルビン関数bei xの近似を評価します。 |
| kelvin_ber(x) | ケルビン関数ber xの近似を評価します。 |
| kelvin_kei(x) | ケルビン関数kei xの近似を評価します。 |
| kelvin_ker(x) | ケルビン関数ker xの近似を評価します。 |
| 名前 | 説明 |
|---|---|
| jacobian_theta(k,x,q) | NAGヤコビのテータ関数。実数引数xおよび負でないq ≤ 1について、ヤコビのテータ関数 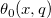 、 、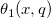 、 、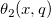 、 、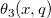 、 、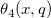 のいずれかの値を計算します。 のいずれかの値を計算します。
|
| lambertW(x[,branch,offset]) | ランベルトのW関数の実数ブランチの近似値を計算します。 |
このカテゴリの複数のパラメータを持つ関数は、組込関数として、非線形フィットなどに使用されます。NLFitを開く(解析:フィット:非線形曲線フィット)と、数式、サンプル曲線、各パラメータ関数に関する詳細を確認できます。そして、関数選択ページから関数を選択します。
Originの非線形フィットから利用できる複数パラメータ関数の詳細については、 OriginLab ウェブサイトにあるPDFファイルをご覧下さい。このファイルでは、各複数パラメータ関数についての数学的な説明、サンプル曲線、パラメータについての解説、LabTalk関数のシンタックスが記載されています。
| 名前 | 説明 |
|---|---|
| Allometric1(x,a,b) | 古典的なFreundlichモデル。相対成長の研究で使われます。
|
| Beta(x,y0,xc,A,w1,w2,w3) | クロマトグラフィと分光法で使われるBeta ピーク関数。
|
| Boltzmann(x, A1, A2, x0, dx) | Boltzmann関数 - シグモイド曲線を生成します。
|
| dhyperbl(x,P1,P2,P3,P4,P5) | 二重直角双曲線関数。
|
| ExpAssoc(x,y0,A1,t1,A2,t2) | 2次の指数関連等式
|
| ExpDec1(x,y0,A1,t1) | 一定時間パラメータの1次指数減少関数
|
| ExpDec2(x,y0,A1,t1,A2,t2) | 一定時間パラメータの2次指数減少関数
|
| ExpDec3(x,y0,A1,t1,A2,t2,A3,t3) | 一定時間パラメータの3次指数減少関数
|
| ExpGrow1(x,y0,x0,A1,t1) | 時間オフセット付き1次指数増加関数。x0は固定。
|
| ExpGrow2(x, y0, x0, A1, t1, A2, t2) | 時間オフセット付き2次指数増加関数。x0は固定。
|
| Gauss(x, y0, xc, w, A) | ガウス関数の面積バージョン (y0 = オフセット, xc = 中心, w = 幅, A = 面積) |
| GaussAmp(x,y0,xc,w,A) | ガウスピーク関数の振幅バージョン (y0 = オフセット, xc = 中心, w = 幅, A = 振幅) |
| Hyperbl(x, P1, P2) | 双曲線関数、酵素反応速度論のMichaelis-Mentenモデル
|
| Logistic(x, A1, A2, x0, p) | 薬理学/化学でのロジスティック用量応答。4PL または 4PLC とも呼ばれます。
|
| LogNormal(x,y0,xc,w,A) | 対数が正規分布するランダム変数の確率密度関数
|
| Lorentz(x, y0, xc, w, A) | ベル型でGaussian関数より幅の広いLorentzianピーク関数
(y0 = オフセット, xc = 中心, w = FWHM, A = 面積) |
| Poisson(x,y0,r) | Poisson確率密度関数。離散確率分布
|
| Pulse(x, y0, x0, A, t1, P, t2) | 指数パルス関数(x >= x0 ? y : 0)
|
| Rational0(x,a,b,c) | 1次の分子と1次の分母を持つRational関数
|
| Sine(x,y0,xc,w,A) | 特定の値の周囲で振動するSin波関数
|
| Voigt(x,y0,xc,A,wG,wL) | Gaussian関数とLorentzian関数のコンボリューション (y0 = オフセット, xc = 中心, A =面積, wG = Gaussian FWHM, wL = Lorentzian FWHM) |
| 名前 | 説明 |
|---|---|
| Circle(x,y,xc,yc,r) | 円中心と半径のパラメータの陰円関数
|
| Ellipse(x,y,xc,yc,a,b) | XY軸と一致する主軸副軸の陰楕円関数
|
| ModDiode(V,I,T,Is,Rs,n,Rsh) | 暗黙的に修正されたダイオード方程式
|
| PlaneMod(x,y,z,theta,phi,d) | 正規方向で定義された修正陰平面関数
|
| SolarCellIV(V,I,T,Is,Rs,n,Rsh,IL) | 太陽電池のI-V曲線
|
| 名前 | 説明 |
|---|---|
| Asymptotic1(x,a,b,c) | Asymptotic回帰モデル- 1次パラメータ
|
| BoxLucas1(x,a,b) | 0オフセットの1次結合関数に等しいBox Lucasモデル
|
| BoxLucas1Mod(x,a,b) | Box Lucasモデルのパラメータ化
|
| BoxLucas2(x,a1,a2) | 2次のBox Lucasモデル
|
| Chapman(x,a,b,c) | 累積成長曲線を説明するChapman-Richards関数
|
| Exp1p1(x,A) | 1つのパラメータの指数関数
|
| Exp1p2(x,A) | 1つのパラメータの指数関数
|
| Exp1p2Md(x,B) | 1つのパラメータの指数関数
|
| Exp1P3(x,A) | 1つのパラメータの指数関数
|
| Exp1P3Md(x,B) | 1つのパラメータの指数関数
|
| Exp1P4(x,A), | 1つのパラメータの漸近指数関数
|
| Exp1P4Md(x,B) | 1つのパラメータの漸近指数関数の変形
|
| Exp2P(x,a,b) | 2つのパラメータの指数関数
|
| Exp2PMod1(x,a,b), | 2つのパラメータの指数関数
|
| Exp2PMod2(x,a,b), | 2つのパラメータの指数関数
|
| Exp3P1(x,a,b,c), | 指数関数の逆オフセット
|
| Exp3P1Md(x,a,b,c), | 指数関数の逆オフセットの別の形
|
| Exp3P2(x,a,b,c), | べき指数が2次の多項式の指数関数
|
| ExpAssoc(x,y0,A1,t1,A2,t2) | 2次の指数関連等式
|
| ExpAssoc1(x,TD,Yb,A,Tau)
(2017 SR0) |
1次の指数関連等式
|
| ExpAssoc2(x,TD1,TD2,Yb,A1,A2,Tau1,Tau2)
(2017 SR0) |
二相指数関連方程式
|
| ExpAssocDelay1(x,TD,Yb,A,Tau)
(2017 SR0) |
指数関数が始まる前のプラトーを用いた一相指数関数方程式
|
| ExpAssocDelay2(x,TD1,TD2,Yb,A1,A2,Tau1,Tau2)
(2017 SR0) |
指数関数が始まる前のプラトーを用いた二相指数関数方程式
|
| Exponential(x,y0,A,R0) | 一定率パラメータの指数増加関数
|
| ExpDec1(x,y0,A1,t1) | 一定時間パラメータの1次指数減少関数
|
| ExpDec2(x,y0,A1,t1,A2,t2) | 一定時間パラメータの2次指数減少関数
|
| ExpDec3(x,y0,A1,t1,A2,t2,A3,t3) | 一定時間パラメータの3次指数減少関数
|
| ExpDecay1(x,y0,x0,A1,t1) | 時間オフセット付き1次指数減少 。x0は修正。
|
| ExpDecay2(x, y0, x0, A1, t1, A2, t2) | 時間オフセット付き2次指数減少 。x0は修正。
|
| ExpDecay3(x,y0,x0,A1,t1,A2,t2,A3,t3) | 時間オフセット付き3次指数減少 。x0は修正。
|
| ExpGro1(x,y0,A1,t1) | 一定時間パラメータの1次指数増加関数
|
| ExpGro2(x,y0,A1,t1,A2,t2) | 一定時間パラメータの2次指数増加関数
|
| ExpGro3(x,y0,A1,t1,A2,t2,A3,t3) | 一定時間パラメータの3次指数減少関数
|
| ExpGrow1(x,y0,x0,A1,t1) | 時間オフセット付き1次指数増加関数。x0は固定。
|
| ExpGrow2(x, y0, x0, A1, t1, A2, t2) | 時間オフセット付き2次指数増加関数。x0は固定。
|
| ExpGrow3Dec2(x,y0,xc,Ag1,tg1,Ag2,tg2,Ag3,tg3,Ad1,td1,Ad2,td2)
(2015 SR0) |
3つの成長と2つの減衰を伴う指数関数。
|
| ExpGrowDec(x,y0,xc,Ag,tg,Ad,td)
(2015 SR0) |
1つの成長と1つの減衰を伴う指数関数。
|
| ExpLinear(x,p1,p2,p3,p4) | 指数と線形の組合せ
|
| Langevin(x,y0,xc,C) | 3つのパラメータの常磁性で使用するLangevin 関数
|
| LangevinMod(x,y0,xc,C,s)
(2015 SR0) |
スケール修正 Langevin関数
|
| PIPlatt(x,Pm,alpha)
(2017 SR0) |
Plattによる光合成−光曲線モデル
|
| PIPlatt2(x,Ps,alpha,beta)
(2017 SR0) |
Plattによる光阻害のある光合成−光曲線モデル
|
| PIWebb(x,Pm,alpha)
(2017 SR0) |
Webbによる光合成−光曲線モデル
|
| MnMolecular(x,A,xc,k), | 単分子の成長関数
|
| MnMolecular1(x,A1,A2,k) | 単分子の成長関数の別の形
|
| Shah(x,a,b,c,r) | 線形関数を統合した指数減少関数
|
| Stirling(x,a,b,k) | パラメータとしてゼロにおける傾きの指数増加関数
|
| YldFert(x,a,b,r) | 農業での収穫肥料モデル、心理学での学習曲線
|
| YldFert1(x,a,b,k) | 農業での収穫肥料モデル、心理学での学習曲線
|
| 名前 | 説明 |
|---|---|
| BiDoseResp(x,A1,A2,LOGx01,LOGx02,h1,h2,p) | 二相容量応答関数
|
| BiHill(x,Pm,Ka,Ki,Ha,Hi)
(2015 SR0) |
二相ヒル関数
|
| BoltzIV(x,vhalf,dx,gmax,vrev) | IVデータに対する変換済みボルツマン関数
|
| Boltzmann(x, A1, A2, x0, dx) | Boltzmann関数 - シグモイド曲線を生成します。
|
| DoseResp(x,A1,A2,LOGx0,p) | パラメータ'p'によって与えられた変数Hill傾きの容量応答曲線
|
| DoubleBoltzmann(x,y0,A,frac,x01,x02,k1,k2) | 二重Boltzmann関数。2つのBoltzmann関数の合計
|
| Hill(x,Vmax,k,n) | 配位子濃度と結合部位の最大数を決定するHill関数
|
| Hill1(x,START,END,k,n) | オフセット付きの修正Hill関数
|
| Logistic(x, A1, A2, x0, p) | 薬理学/化学でのロジスティック用量応答。4PL または 4PLC とも呼ばれます。
|
| Logistic5(x,Amin,Amax,x0,h,s) | 5つのパラメータを持つ、ロジスティック関数。5PL または 5PLC とも呼ばれます。
|
| MichaelisMenten(x,Vmax,Km) | 酵素動力学の基本モデル。単一基質 Michaelis-Menten関数。
|
| SGompertz(x,a,xc,k) | 動物の成長や人口増加の研究でのGompertz成長モデル
|
| Slogistic1(x,a,xc,k) | タイプ1のシグモイドロジスティック関数
|
| SLogistic2(x,y0,a,Wmax) | タイプ2のシグモイドロジスティック関数
|
| SLogistic3(x,a,b,k) | タイプ3のシグモイドロジスティック関数
|
| SRichards1(x,a,xc,d,k) | タイプ1のシグモイドリチャード関数
|
| SRichards2(x,a,xc,d,k) | タイプ2のシグモイドリチャード関数
|
| SWeibull1(x,A,xc,d,k) | タイプ1のシグモイドワイブル関数
|
| SWeibull2(x,a,b,d,k) | タイプ2のシグモイドワイブル関数
|
| 名前 | 説明 |
|---|---|
| Dhyperbl(x,P1,P2,P3,P4,P5) | 二重直角双曲線関数。
|
| Hyperbl(x, P1, P2) | 双曲線関数、酵素反応速度論のMichaelis-Mentenモデル
|
| HyperbolaGen(x,a,b,c,d) | 一般化双曲線関数
|
| HyperbolaMod(x,T1,T2) | 修正双曲線関数
|
| RectHyperbola(x,a,b) | 直角双曲線関数。
|
| 名前 | 説明 |
|---|---|
| Bradley(x,a,b) | 二重対数相互関数
|
| Log2P1(x,a,b), | 2つのパラメータの対数関数
|
| Log2P2(x,a,b) | 対数変換関数
|
| Log3P1(x,a,b,c) | 線形対数変換関数
|
| Logarithm(x,A) | 1つのパラメータの対数関数
|
| 名前 | 説明 |
|---|---|
| Asym2Sig(x,y0,xc,A,w1,w2,w3) | 非対称の2重シグモイド
|
| Beta(x,y0,xc,A,w1,w2,w3) | クロマトグラフィと分光法で使われるBeta ピーク関数。
|
| Bigaussian(x,y0,xc,H,w1,w2) | 非対称ピークのフィットに使用する二重Gaussianピーク関数
|
| CCE(x,y0,xc1,A,w,k2,xc2,B,k3,xc3) | クロマトグラフィで使われるChesler-Cramピーク関数
|
| ECS(x,y0,xc,A,w,a3,a4) | クロマトグラフィで使われるEdgeworth-Cramerピーク関数
|
| Extreme(x,y0,xc,w,A) | 特例のExtreme関数。Gumbel確率密度関数
|
| Gauss(x, y0, xc, w, A) | ガウス関数の面積バージョン (y0 = オフセット, xc = 中心, w = 幅, A = 面積) |
| GaussAmp(x,y0,xc,w,A) | ガウスピーク関数の振幅バージョン (y0 = オフセット, xc = 中心, w = 幅, A = 振幅) |
| Gaussian(x,y0,xc,A,w) | ガウス関数のFWHMバージョン (y0 = ベースライン, xc = 中心, A = 面積, w = FWHM) |
| GaussMod(x,y0,A,xc,w,t0) | クロマトグラフィで使用される指数修正ガウス(EMG)ピーク関数
|
| GCAS(x,y0,xc,A,w,a3,a4) | クロマトグラフィで使われるGram-Charlierピーク関数
|
| Giddings(x,y0,xc,w,A) | クロマトグラフィで使われるGiddingsrピーク関数
|
| InvsPoly(x,y0,xc,w,A,A1,A2,A3) | 中心の逆多項式ピーク関数
|
| Laplace(x,y0,a,b) | ラプラス確率密度関数
|
| Logistpk(x,y0,xc,w,A) | ロジスティックピーク関数。Hubbert関数とも呼ばれる。
|
| LogNormal(x,y0,xc,w,A) | 対数が正規分布するランダム変数の確率密度関数
|
| Lorentz(x, y0, xc, w, A) | ベル型でGaussian関数より幅の広いLorentzianピーク関数 (y0 = オフセット, xc = 中心, w = FWHM, A = 面積) |
| PearsonIV(x,y0,A,m,v,alpha,lam) | 負の判別子のためのピアソンのタイプIV分布。偏りのある分布に適合しやすい。
|
| PearsonVII(x,y0,xc,A,w,m) | ピアソンのタイプVIIピーク関数、べき乗されたローレンツ関数。
|
| PsdVoigt1(x,y0,xc,A,w,mu) | 擬フォークト(Pseudo-Voigt)関数。Gaussian関数とLorentzian関数の線形混合 (y0 = オフセット, xc = 中心, A = 面積, w = FWHM, mu = プロファイル形要因) |
| PsdVoigt2(x,y0,xc,A,wG,wL,mu) | 擬フォークト(Pseudo-Voigt)関数。異なるFWHMのGaussian関数とLorentzian関数の線形混合 (y0 = オフセット, xc = 中心, A =面積, wG=Gaussian FWHM, wL=Lorentzian FWHM, mu = プロファイル形要因) |
| Voigt(x,y0,xc,A,wG,wL) | Gaussian関数(wG は FWHM) と Lorentzian 関数のコンボリューション
|
| Weibull3(x,y0,xc,A,w1,w2) | ワイブルピーク関数の振幅バージョン
|
| 名前 | 説明 |
|---|---|
| PWL2(x,a1,k1,xi,k2) | 2つの区分のPiecewise線形関数
|
| PWL3(x,a1,k1,xi1,k2,xi2,k3) | 3つの区分のPiecewise線形関数
|
| 名前 | 説明 |
|---|---|
| Constant(x,y0) | 定数の線形関数
|
| Cubic(x,A,B,C,D) | 3次の多項式
|
| Line(x,A,B) | 傾きと切片を持つ線形関数
|
| LineMod(x,a,b) | X切片と傾きを持つ線形関数
|
| Parabola(x,A,B,C) | 2次の多項式
|
| Poly(x, a0, a1, a2, a3, a4, a5, a6, a7, a8, a9) | 9次の多項式
|
| Poly4(x,A0,A1,A2,A3,A4) | 4次多項式関数
|
| Poly5(x,A0,A1,A2,A3,A4,A5) | 5次多項式関数
|
| 名前 | 説明 |
|---|---|
| Allometric1(x,a,b) | 古典的なFreundlichモデル。相対成長の研究で使われます。
|
| Allometric2(x,a,b,c) | 古典的なFreundlichモデル。
|
| Belehradek(x,a,b,c) | Xがシフトしたべき関数
|
| BlNeld(x,a,b,c,f) | 収量密度モデルのBleasdale-Nelder関数
|
| BlNeldSmp(x,a,b,c) | 単純化Bleasdale-Nelder モデル
|
| FarazdaghiHarris(x,a,b,c) | 収量密度研究で使われるFarazdaghi-Harrisモデル
|
| FreundlichEXT(x,a,b,c) | 拡張Freundlich 吸着等温式
|
| Gunary(x,a,b,c) | Gunary 吸着等温式
|
| LangmuirEXT1(x,a,b,c), | 拡張Langmuir吸着等温式
|
| LangmuirEXT2(x,a,b,c) | 拡張Langmuir吸着等温式の変形
|
| Pareto(x,A) | 1つのパラメータのPareto累積密度関数。冪乗則確率分布
|
| Pow2P1(x,a,b), | スケールされたPareto関数
|
| Pow2P2(x,a,b), | 2つのパラメータのpower関数
|
| Pow2P3(x,a,b) | Pareto変換関数
|
| Power(x,A) | 1つのパラメータのpower関数
|
| Power0(x,y0,xc,A,P) | オフセット付きの対称Power関数
|
| Power1(x,xc,A,P) | 対称Power関数
|
| Power2(x,xc,A,pl,pu) | 非対称Power関数
|
| 名前 | 説明 |
|---|---|
| BET(x,a,b) | Brunauer-Emmett-Teller (BET) 吸着式
|
| BETMod(x,a,b) | 修正BETモデル
|
| Holliday(x,a,b,c) | Holliday モデル - 農業で使われる収穫密度モデル
|
| Holliday1(x,a,b,c) | 拡張Hollidayモデル
|
| Nelder(x,a,b0,b1,b2) | Nelder モデル - 農業で使われる収穫-肥料モデル
|
| Rational0(x,a,b,c) | 1次の分子と1次の分母を持つRational関数
|
| Rational1(x,a,b,c) | 一定係数で標準化した分子のRational0関数の別の形
|
| Rational2(x,a,b,c) | xの係数で標準化した分母のRational0関数の別の形
|
| Rational3(x,a,b,c) | x係数で標準化した分子のRational0関数の別の形
|
| Rational4(x,a,b,c) | 定数とrational関数の合計付きRational0関数の別の形
|
| Rational5(x,a,b,c,d) | 1次の分子と2次の分母を持つRational関数
|
| Reciprocal(x,a,b) | 2つのパラメータの線形逆数関数
|
| Reciprocal0(x,A) | 1つのパラメータ(傾き)の線形逆数関数
|
| Reciprocal1(x,A) | 1つのパラメータ(切片)の線形逆数関数
|
| ReciprocalMod(x,a,b) | 一定係数で標準化した分母のReciprocal関数の別の形
|
| 名前 | 説明 |
|---|---|
| SawtoothWave(x,x0,y0,A,T) | のこぎり波。非対称な三角形の波で構成される周期関数。
|
| Sine(x,y0,xc,w,A) | 特定の値の周囲で振動するSin波関数
|
| SineDamp(x,y0,xc,w,t0,A) | 正弦波収束関数。時間経過とともに振幅が減少する正弦波関数
|
| SineSqr(x,y0,xc,w,A) | Sin二乗関数
|
| SquareWave(x,a,b,x0,T) | 2つのレベルで周期的に変化する矩形波関数
|
| SquareWaveMod(x, a, b, x0, duty, T)
(2016 SR0) |
2つのレベルで周期的に変化する矩形波関数
|
| Step(x,A,B,x1) | 2つの区分のPiecewise 定数関数
|
| 名前 | 説明 |
|---|---|
| Asym2Sig(x,y0,xc,A,w1,w2,w3) | 非対称の2重シグモイド
|
| Bigaussian(x,y0,xc,H,w1,w2) | 非対称ピークのフィットに使用する二重Gaussianピーク関数
|
| BWF(x,y0,xc,H,w,q) | Breit-Wigner-Fano (BWF) 線形
|
| CCE(x,y0,xc1,A,w,k2,xc2,B,k3,xc3) | クロマトグラフィで使われるChesler-Cramピーク関数
|
| ConsGaussian(x,y0, xc, A, w1, w2) | 制約付きGaussian関数
|
| DoniachSunjic(x,y0, xc, H, w, a) | Doniach Sunjic関数
|
| ECS(x,y0,xc,A,w,a3,a4) | クロマトグラフィで使われるEdgeworth-Cramerピーク関数
|
| FraserSuzuki(x,y0,xc,A,sig) | FraserSuzuki 非対称関数
ここで
|
| Gauss(x, y0, xc, w, A) | ガウス関数の面積バージョン (y0 = オフセット, xc = 中心, w = 幅, A = 面積) |
| GaussAmp(x,y0,xc,w,A) | ガウスピーク関数の振幅バージョン (y0 = オフセット, xc = 中心, w = 幅, A = 振幅) |
| Gaussian(x,y0,xc,A,w) | ガウス関数のFWHMバージョン (y0 = ベースライン, xc = 中心, A = 面積, w = FWHM) |
| Gaussian_LorenCross(x,y0, xc, A, w, s) | Gaussian-Lorentzian クロス積
|
| GaussMod(x,y0,A,xc,w,t0) | クロマトグラフィで使用される指数修正ガウス(EMG)ピーク関数
|
| GCAS(x,y0,xc,A,w,a3,a4) | クロマトグラフィで使われるGram-Charlierピーク関数
|
| HVL(x, y0, xc, A, w, d) | Haaroff-Van der Linde 関数
|
| InvsPoly(x,y0,xc,w,A,A1,A2,A3) | 中心の逆多項式ピーク関数
|
| LogNormal(x,y0,xc,w,A) | 対数が正規分布するランダム変数の確率密度関数
|
| Lorentz(x, y0, xc, w, A) | ベル型でGaussian関数より幅の広いLorentzianピーク関数 (y0 = オフセット, xc = 中心, w = FWHM, A = 面積) |
| PearsonVII(x,y0,xc,A,w,m) | ピアソンのタイプVIIピーク関数、べき乗されたローレンツ関数。
|
| PsdVoigt1(x,y0,xc,A,w,mu) | 擬フォークト(Pseudo-Voigt)関数。Gaussian関数とLorentzian関数の線形混合 (y0 = オフセット, xc = 中心, A = 面積, w = FWHM, mu = プロファイル形要因) |
| PsdVoigt2(x,y0,xc,A,wG,wL,mu) | 擬フォークト(Pseudo-Voigt)関数。異なるFWHMのGaussian関数とLorentzian関数の線形混合 (y0 = オフセット, xc = 中心, A =面積, wG=Gaussian FWHM, wL=Lorentzian FWHM, mu = プロファイル形要因) |
| Pulse(x,y0,x0,A,t1,P,t2) | 指数パルス関数(x >= x0 ? y : 0)
|
| SchulzFlory(x,y0,xc,w,A) | 重合の後ポリマーの相関的比率を説明するためのSchulz Flory分布関数
|
| Sine(x,xc,w,A,y0) | 特定の値の周囲で振動するSin波関数
|
| SineDamp(x,y0,xc,w,t0,A) | 正弦波収束関数。時間経過とともに振幅が減少する正弦波関数
|
| Sinesqr(x,xc,w,A,y0) | Sin二乗関数
|
| Voigt(x,y0,xc,A,wG,wL) | Gaussian関数(wG は FWHM) と Lorentzian 関数のコンボリューション (y0 = オフセット, xc = 中心, A =面積, wG = Gaussian FWHM, wL = Lorentzian FWHM) |
| Weibull3(x,y0,xc,A,w1,w2) | ワイブルピーク関数の振幅バージョン
|
| 名前 | 説明 |
|---|---|
| Constant(x,y0) | 定数の線形関数
|
| Cubic(x,A,B,C,D) | 3次の多項式
|
| ExpDec1(x,y0,A1,t1) | 一定時間パラメータの1次指数減少関数
|
| ExpDec2(x,y0,A1,t1,A2,t2) | 一定時間パラメータの2次指数減少関数
|
| ExpGro1(x,y0,A1,t1) | 一定時間パラメータの1次指数増加関数
|
| ExpGrow1(x,y0,x0,A1,t1) | 時間オフセット付き1次指数増加関数。x0は固定。
|
| ExpGrow2(x, y0, x0, A1, t1, A2, t2) | 時間オフセット付き2次指数増加関数。x0は固定。
|
| Exponential(x,y0,A,R0) | 一定率パラメータの指数増加関数
|
| Hyperbl(x, P1, P2) | 双曲線関数、酵素反応速度論のMichaelis-Mentenモデル
|
| Line(x,A,B) | 傾きと切片を持つ線形関数
|
| MnMolecular(x,A,xc,k), | 単分子の成長関数
|
| Parabola(x,A,B,C) | 2次の多項式
|
| Poly4(x,A0,A1,A2,A3,A4) | 4次多項式関数
|
| Poly5(x,A0,A1,A2,A3,A4,A5) | 5次多項式関数
|
| Step(x,A,B,x1) | 2つの区分のPiecewise 定数関数
|
| 名前 | 説明 |
|---|---|
| CCE(x,y0,xc1,A,w,k2,xc2,B,k3,xc3) | クロマトグラフィで使われるChesler-Cramピーク関数
|
| ECS(x,y0,xc,A,w,a3,a4) | クロマトグラフィで使われるEdgeworth-Cramerピーク関数
|
| Gauss(x, y0, xc, w, A) | ガウス関数の面積バージョン (y0 = オフセット, xc = 中心, w = 幅, A = 面積) |
| GaussMod(x,y0,A,xc,w,t0) | クロマトグラフィで使用される指数修正ガウス(EMG)ピーク関数
|
| GCAS(x,y0,xc,A,w,a3,a4) | クロマトグラフィで使われるGram-Charlierピーク関数
|
| Giddings(x,y0,xc,w,A) | クロマトグラフィで使われるGiddingsrピーク関数
|
| 名前 | 説明 |
|---|---|
| BoltzIV(x,vhalf,dx,gmax,vrev) | IVデータに対する変換済みボルツマン関数
|
| Boltzmann(x, A1, A2, x0, dx) | Boltzmann関数 - シグモイド曲線を生成します。
|
| DoubleBoltzmann(x,y0,A,frac,x01,x02,k1,k2) | 二重Boltzmann関数。2つのBoltzmann関数の合計
|
| ExpDec1(x,y0,A1,t1) | 一定時間パラメータの1次指数減少関数
|
| ExpDec2(x,y0,A1,t1,A2,t2) | 一定時間パラメータの2次指数減少関数
|
| ExpDec3(x,y0,A1,t1,A2,t2,A3,t3) | 一定時間パラメータの3次指数減少関数
|
| Gauss(x, y0, xc, w, A) | ガウス関数の面積バージョン (y0 = オフセット, xc = 中心, w = 幅, A = 面積) |
| Goldman(x,b,Nao,Nai,Ki,T) | 電気生理学のGoldman-Hodgkin-Katz の式
|
| Hill(x,Vmax,k,n) | 配位子濃度と結合部位の最大数を決定するHill関数
|
| 名前 | 説明 |
|---|---|
| BiDoseResp(x,A1,A2,LOGx01,LOGx02,h1,h2,p) | 二相容量応答関数
|
| Biphasic(x,Amin,Amax1,Amax2,x0_1,x0_2,h1,h2) | 二相シグモイド用量反応(7つのパラメータのロジスティック方程式)
|
| DoseResp(x,A1,A2,LOGx0,p) | パラメータ'p'によって与えられた変数Hill傾きの容量応答曲線
|
| MichaelisMenten(x,Vmax,Km) | 酵素動力学の基本モデル。単一基質 Michaelis-Menten関数。
|
| OneSiteBind(x,Bmax,k1) | 片側直接結合。直角双曲線が等温線や飽和率曲線に接続します。
|
| OneSiteComp(x,A1,A2,logx0) | 片側競争曲線。Hill傾斜が-1のDose-response曲線
|
| TwoSiteBind(x,Bmax1,Bmax2,k1,k2) | 両側結合関数
|
| TwoSiteComp(x,A1,A2,logx0_1,logx0_2,fraction) | 2種の受容器のための配位子の競合を説明する両側競合関数
|
| 名前 | 説明 |
|---|---|
| Bingham(x,y0,A)
(2015 SR0) |
降伏応答を示す粘塑性流体を記述するBinghamモデル。
|
| Cross(x,A1,A2,t,m)
(2015 SR0) |
ゼロおよび無限のせん断速度で漸近粘度をもつ擬塑性流動を記述するクロスモデル。
|
| Carreau(x,A1,A2,t,a,n)
(2015 SR0) |
ゼロおよび無限のせん断速度で漸近粘度をもつ擬塑性流動を記述するCarreau-Yasudaモデル。
|
| Herschel(x,y0,K,n)
(2015 SR0) |
ベキ乗関係を示す粘塑性材料を記述する Herschel-Bulkley モデル
|
| VFT(x,A,B,x0)
(2015 SR0) |
Vogel-Fulcher-Tammannの式
|
| MYEGA(x,y0,K,C)
(2015 SR0) |
Mauro-Yue-Ellison-Gupta-Allanの式
|
| 名前 | 説明 |
|---|---|
| CompInhib(x,Vmax,Km,Ki,Ic)
(2015 SR0) |
1つの基盤と1つの阻害の競合阻害モデル
|
| NoncompInhib(x,Vmax,Km,Ki,Ic)
(2015 SR0) |
1つの基盤と1つの阻害の非競合阻害モデル
|
| UncompInhib(x,Vmax,Km,Kia,Ic)
(2015 SR0) |
1つの基盤と1つの阻害の不競合阻害モデル
|
| MixedModelInhib(x,Vmax,Km,Ki,Alpha,Ic)
(2015 SR0) |
特殊なケースとして、競合、不競合および非競合阻害を含む一般的な方程式。
|
| SubstrateInhib(x,Vmax,Km,Ki)
(2015 SR0) |
高濃度の基質阻害モデル
|
| MichaelisMenten(x,Vmax,Km) | 酵素動力学の基本モデル。単一基質 Michaelis-Menten関数。
|
| Hill(x,Vmax,k,n) | 配位子濃度と結合部位の最大数を決定するHill関数
|
| 名前 | 説明 |
|---|---|
| GaussAmp(x,y0,xc,w,A) | ガウスピーク関数の振幅バージョン (y0 = オフセット, xc = 中心, w = 幅, A = 振幅) |
| InvsPoly(x,y0,xc,w,A,A1,A2,A3) | 中心の逆多項式ピーク関数
|
| Lorentz(x, y0, xc, w, A) | ベル型でGaussian関数より幅の広いLorentzianピーク関数 (y0 = オフセット, xc = 中心, w = FWHM, A = 面積) |
| PearsonVII(x,y0,xc,A,w,m) | ピアソンのタイプVIIピーク関数、べき乗されたローレンツ関数。
|
| PsdVoigt1(x,y0,xc,A,w,mu) | 擬フォークト(Pseudo-Voigt)関数。Gaussian関数とLorentzian関数の線形混合 (y0 = オフセット, xc = 中心, A = 面積, w = FWHM, mu = プロファイル形要因) |
| PsdVoigt2(x,y0,xc,A,wG,wL,mu) | 擬フォークト(Pseudo-Voigt)関数。異なるFWHMのGaussian関数とLorentzian関数の線形混合 (y0 = オフセット, xc = 中心, A =面積, wG=Gaussian FWHM, wL=Lorentzian FWHM, mu = プロファイル形要因) |
| Voigt(x,y0,xc,A,wG,wL) | Gaussian関数(wG は FWHM) と Lorentzian 関数のコンボリューション
|
| 名前 | 説明 |
|---|---|
| Exponential(x,y0,A,R0) | 一定率パラメータの指数増加関数
|
| ExponentialCDF(x,y0,A,mu)
(2016 SR0) |
Exponential 累積分布関数
|
| Extreme(x,y0,xc,w,A) | 特例のExtreme関数。Gumbel確率密度関数
|
| GammaCDF(x,y0,A1,a,b)
(2016 SR0) |
Gamma 累積分布関数
|
| Gauss(x, y0, xc, w, A) | ガウス関数の面積バージョン (y0 = オフセット, xc = 中心, w = 幅, A = 面積) |
| GaussAmp(x,y0,xc,w,A) | ガウスピーク関数の振幅バージョン (y0 = オフセット, xc = 中心, w = 幅, A = 振幅) |
| Gumbel(x,a,b) | 変換Gumbel累積分布関数
|
| Laplace(x,y0,a,b) | ラプラス確率密度関数
|
| Logistic(x, A1, A2, x0, p) | 薬理学/化学でのロジスティック用量応答。4PL または 4PLC とも呼ばれます。
|
| LogNormal(x,y0,xc,w,A) | 対数が正規分布するランダム変数の確率密度関数
|
| LognormalCDF(x,y0,A,xc,w)
(2016 SR0) |
LognormalCDF 累積分布関数
|
| Lorentz(x, y0, xc, w, A) | ベル型でGaussian関数より幅の広いLorentzianピーク関数 (y0 = オフセット, xc = 中心, w = FWHM, A = 面積) |
| NormalCDF(x,y0,A,xc,w) | 通常の累積分布関数 ( y0 = オフセット, A = 振幅, xc = 平均, w = 標準偏差) |
| Pareto(x,A) | 1つのパラメータのPareto累積密度関数。冪乗則確率分布
|
| Pareto2(x,a,b) | 2つのパラメータのPareto関数
|
| PearsonIV(x,y0,A,m,v,alpha,lam) | 負の判別子のためのピアソンのタイプIV分布。偏りのある分布に適合しやすい。
|
| Poisson(x,y0,r) | Poisson確率密度関数。離散確率分布
|
| Rayleigh(x,b) | Rayleigh 累積分布関数
|
| Weibull(x,y0,a,r,u) | Weibull確率密度関数
|
| WeibullCDF(x,y0,A1,a,b)
(2016 SR0) |
Weibull累積分布関数
|
| 名前 | 説明 |
|---|---|
| Boltzmann(x, A1, A2, x0, dx) | Boltzmann関数 - シグモイド曲線を生成します。
|
| DoseResp(x,A1,A2,LOGx0,p) | パラメータ'p'によって与えられた変数Hill傾きの容量応答曲線
|
| ExpDecay1(x,y0,x0,A1,t1) | 時間オフセット付き1次指数減少 。x0は修正。
|
| ExpGrow1(x,y0,x0,A1,t1) | 時間オフセット付き1次指数増加関数。x0は固定。
|
| Gauss(x, y0, xc, w, A) | ガウス関数の面積バージョン (y0 = オフセット, xc = 中心, w = 幅, A = 面積) |
| Hill(x,Vmax,k,n) | 配位子濃度と結合部位の最大数を決定するHill関数
|
| Hyperbl(x, P1, P2) | 双曲線関数、酵素反応速度論のMichaelis-Mentenモデル
|
| Logistic(x, A1, A2, x0, p) | 薬理学/化学でのロジスティック用量応答。4PL または 4PLC とも呼ばれます。
|
| Lorentz(x, y0, xc, w, A) | ベル型でGaussian関数より幅の広いLorentzianピーク関数 (y0 = オフセット, xc = 中心, w = FWHM, A = 面積) |
| Sine(x,y0,xc,w,A) | 特定の値の周囲で振動するSin波関数
|
| Voigt(x,y0,xc,A,wG,wL) | Gaussian関数(wG は FWHM) と Lorentzian 関数のコンボリューション
|
| 名前 | 説明 |
|---|---|
| GaussianLorentz(y0, xc, A1, A2, w1, w2) | 1つの独立変数と2つの従属変数、共有パラメータ
|
| Helix(x,x0,y0,A,w,p) | 3D Helix 関数
|
| HillBurk(Vm1, Km1, Vm2, Km2) | 2つの独立した変数と2つの従属変数を持つHillとBurkモデルの組み合わせ。
|
| Line3(a, b, c, d) | 傾斜と切片を持つ3D Line関数
|
| LineExp(x,Vmax,k,n) | 1つの独立変数と2つの従属変数を持つ線と指数モデルの組み合わせ。
|
| 名前 | 説明 |
|---|---|
| BitAND(n1, n2) | 2つの整数のビット積を返します。 |
| BitOR(n1, n2) | 2つの整数のビット和を返します。 |
| BitXOR(n1, n2) | 2つの整数のビット排他的和を返します。 |
| ISNA(d) | 数字が NANUMかどうか判定します。 |
| isText(str$)
(2019) |
値がテキストかどうかを判定します。値がテキストかどうかを判定します。テキストの場合1または空欄、数値の場合NANUMを返します。 |
| Let(var1,val1[,var2,val2,]...[,var39, val39], expression)[$]
(2021) |
ExcelのLET()関数に似ています。式で使用するために、最大39の変数と値のペアの変数(valN)に値(varN)を割り当てます。オプションの$は文字列を返すときに使用されます。サンプル:
|
| NA() | NANUMを返します。 |
| ocolor2rgb(oColor)
(2019 SR0) |
内部カラーコードoColorをRGB値に変換します。 |
| xf_get_last_error_code() | Xファンクションエンジンの最後のエラーコードの値を取得します。 |
| xf_get_last_error_message()$ | Xファンクションエンジンの最後のエラーメッセージを取得します。 |
| xor(n1,n2)
(2019 SR0) |
2つの論理値n1とn2のXOR演算を返します。サンプル
|
| 名前 | 説明 |
|---|---|
| Base(num,radix[,len])$
(2019 SR0) |
与えられた整数numを指定された基数の文字列表現に変換します。
radix. |
| Bin2Dec(str$) | 2進数を10進数に変換します。 |
| BitLShift(num,shift)
(2019 SR0) |
指定されたビット数だけシフトした10進数のシフト |
| BitRShift(num,shift)
(2019 SR0) |
指定されたビット数だけシフトした10進数のシフト |
| Convert(d,str1$,str2$) | ある測定系から別の測定系に数値を変換します。 |
| Decimal(text$,radix) | 指定された基数の文字列表現テキスト を10進数に変換します。
10進数 |
| Dec2Bin(n)$ | 0進数を2進数に変換します。入力範囲は-512 から 511に制限されます。 |
| Dec2Hex(n[,places])$ | 10進数を16進数に変換し、オプションで文字数を指定します。 |
| Hex2Dec(str$) | 16進数の文字列表現を10進数に変換します。 |
| 名前 | 説明 |
|---|---|
| Imabs(c) | 複素数の絶対値を取得します。 |
| Imaginary(c) | この関数は、複素数の虚部を取得します。 |
| Imargument(c) | 複素数の引数(シータ)を求めます。 |
| Imatan(c)
(2016 SR0) |
その複素数の逆タンジェントを返します。 |
| Imatanh(c)
(2016 SR0) |
その複素数の逆双曲線正接を返します。 |
| Imconjugate(c) | 複素数の共役を取得します。 |
| Imcos(c) | 複素数のcos値を計算します。
ここでCは複素数で、 |
| Imcosh(c)
(2019 SR0) |
与えられた複素数の双曲線コサインを計算します。 |
| Imcot(c)
(2019 SR0) |
与えられた複素数のコタンジェントを計算する。 |
| Imcsc(c)
(2019 SR0) |
与えられた複素数のコセカントを計算します。 |
| Imcsch(c)
(2019 SR0) |
与えられた複素数の双曲線コセカントを計算します。 |
| Imsec(c)
(2019 SR0) |
与えられた複素数のセカントを計算します。 |
| Imsech(c)
(2019 SR0) |
与えられた複素数の双曲線セカントを計算します。 |
| Imsinh(c)
(2019 SR0) |
与えられた複素数の双曲線サインを計算します。 |
| Imtan(c)
(2019 SR0) |
与えられた複素数のタンジェントを計算する。 |
| Imdiv(c1,c2) | 複素数除算を行います。 |
| Imexp(c) | 複素数の指数値を計算します。
ここで |
| Imln(c) | 複素数の自然対数を計算します。
ここで、ImAbs は、複素数の絶対値を計算します。 |
| Imlog10(c) | 複素数の底10の対数を計算します。
ここで、ImLn は、複素数の自然定数を計算し、 |
| Imlog2(c) | 複素数の底2の対数を計算します。
ここで、ImLn は、複素数の自然定数を計算し、 |
| ImPower(c,d) | 複素数に指定したべき乗を行います。 |
| Improduct(c1,c2) | 2つの複素数の積を求めます(乗算)。
|
| ImReal(c) | 指定した複素数の実数部を取得します。 |
| Imsin(c) | 複素数の正弦値を計算します。
ここでCは複素数で、 |
| Imsqrt(c) | 複素数の平方根を計算します。 |
| ImSub(c1,c2) | 2つの複素数の減算を実行します。 |
| ImSum(c1,c2) | 2つの複素数の合計を求めます。 |
| Real2Complex(real,imag) | 指定した2つ実数を複素数に変換します。出力列のデータ型をcomplex(16)にする必要があります。 例:
|
| 名前 | 説明 |
|---|---|
| Effect(nrate,npery) | 実効年間利率を計算します。 |
| Nominal(erate,npery) | 名目年間利率を計算します。 |
| pDuration(rate,pv,fv) | 投資が必要とする将来価値に達するために必要な期間数を計算します。 |
| RRI(nper, pv, fv) | 投資の成長に対する等価利率を計算します。 |
それぞれの関数は、関数のタイプと与えられた引数により、一つの値、あるいは、ある範囲の値(データセット)のどちらかを返します。そうでない場合、何も指定がなければ、すべての関数は、渡される最初の引数が範囲の場合、範囲を返し、値の場合、値を返します。