![y=\left[ a^{1-d}-e^{-k\left( x-xc\right) }\right] ^{1/\left( 1-d\right) },d<1](../images/SRichards1/math-02da77778d79d2e7df03097beb472504.png "y=\left[ a^{1-d}-e^{-k\left( x-xc\right) }\right] ^{1/\left( 1-d\right) },d<1")
内容 |
![y=\left[ a^{1-d}+e^{-k\left( x-xc\right) }\right] ^{1/\left( 1-d\right) },d>1](../images/SRichards1/math-0b8357b9617cce6713eed5ae4f2ef98b.png "y=\left[ a^{1-d}+e^{-k\left( x-xc\right) }\right] ^{1/\left( 1-d\right) },d>1")
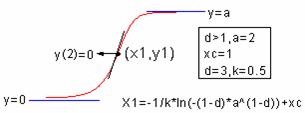
タイプ1のシグモイドリチャード関数
参考文献Seber, G. A. F., Wild, C. J. 1989.Nonlinear Regression.John Wiley & Sons, Inc. pp. 332 - 337
数：4
パラメータの名前:a, xc, d, k
意味:a = unknown, xc = 中心, d = unknown, k = 係数
下側境界:a > 0.0, k > 0.0
上側境界:なし
nlf_srichards1(x,a,xc,d,k)
FITFUNC\SRICHAR1.FDF
Growth/Sigmoidal