各列が別々のデータセットとして扱われます。それぞれのデータで独立した統計操作が実行されます。
全列が1つのデータセットとして扱われます。
実行するデータ範囲を指定します。
- データ範囲
- 入力するデータの範囲です。
- グループ
- 重み範囲
- 重み付け情報を含む範囲です。各セルの値が対応するデータの重みを指定します。
再計算オプションの詳細は、分析結果の再計算を参照してください。
このチェックをつけると、空のデータセットを計算に使用しません。
このチェックをつけると、テキストデータセットを計算に使用しません。
インデックスまたは素データから入力データモードを指定します。
| 独立列 |
各列が別々のデータセットとして扱われます。それぞれのデータで独立した統計操作が実行されます。 |
|---|---|
| 単一データセットに合併する |
全列が1つのデータセットとして扱われます。 |
| 範囲1 |
実行するデータ範囲を指定します。
|
 番目のサンプルを
番目のサンプルを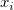 とし、
とし、 番目のサンプルを
番目のサンプルを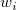 とします。
とします。
| N合計 |
Nで表されるデータポイントの総数 |
|---|---|
| N 欠損 |
欠損値の数 |
| 平均 |
平均(アベレージ)スコア
|
| 標準偏差 |
ここで、 Note: OriginProでは, |
| 平均値のSE | 平均の標準誤差です。
|
| 平均の下側95%信頼区間 |
平均の95%信頼区間の下側限界
ここで、 |
| 平均の上側95%信頼区間 |
平均の95%信頼区間の上側限界
ここで、 |
| 分散 |
|
| 合計 | 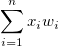 .WEIGHT変数がない場合、式は .WEIGHT変数がない場合、式は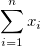 になります。 になります。 |
| 歪度 |
歪度は、分布の非対称性の度合いを測るものです。以下のように定義されています。
Note: WDFおよびWS法が選択されていると、歪度は欠損値として返されます。 |
| 尖度 |
尖度は、分布のとがり具合を表します。
Note: WDFおよびWS法が選択されていると、尖度は欠損値として返されます。 |
| 未修正平方和 |
|
| 修正平方和 |
|
| ばらつきの係数 |
|
| 平均絶対偏差 |
|
| SDの2倍 |
標準偏差の2倍です。
|
| SDの3倍 |
標準偏差の3倍です。
|
| 幾何平均 |
Note: 幾何平均では重みは無視されます。 |
| 幾何SD |
幾何学標準偏差 Note: 幾何標準偏差では重みは無視されます。 |
| モード |
モード(最頻値)は、データ範囲で最も頻繁に表示される要素です。最頻値が複数ある場合は、最小のものが選択されます。 |
| 重みの合計 |
|
| 調和平均 |
調和平均です。
重み付き: 任意の |
分位数は、データからの値で、与えられたセットのデータポイントの所定の割合です。たとえば、任意のデータセットのデータポイントの25%が最初の四分位数より下にあり、データポイントの50%が2番目の四分位数または中央値より下にあります。
入力データセットを昇順で並べ替えます。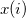 を、並べ替えられたデータセットの
を、並べ替えられたデータセットの 番目の要素とします
番目の要素とします
| 最小値 |
|
|---|---|
| 最小値のインデックス |
元の入力データセットで最小値がある行の番号です。 |
| 第一四分位(Q1) |
第1 (25%) 四分位、Q1です。計算方法については、分位数の補間を参照してください。 |
| 中央値 |
メディアンまたは第2 (50%)四分位、Q2です。計算方法については、分位数の補間を参照してください。 |
| 第3四分位(Q3) |
第3 (75%) 四分位、 Q3です。計算方法については、分位数の補間を参照してください。 |
| 最大 |
|
| 最大値のインデックス |
元の入力データセットで最大値がある行の番号です。 |
| 四分位範囲 (Q3-Q1) |
|
| 範囲 (最大-最小) |
最大 - 最小 |
| カスタムパーセンタイル |
カスタムパーセンタイルを計算する場合チェックを付けます。 |
| パーセンタイルリスト |
このオプションは、カスタムパーセンタイルにチェックが付いている場合にのみ利用できます。ここに入力された全ての値でのパーセンタイルが計算されます。 |
| 中央値の絶対偏差(MAD) | 単変量データセットX1、X2、...、Xnの場合、MADはデータの中央値からの絶対偏差の中央値として定義されます。
つまり、データの中央値からの残差(偏差)で始まる場合、MADは絶対値の中央値です。 |
| ロバスト変動係数 |
|
極値を返します。極値は、最も高い値と最も低い値です。
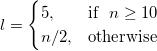
ここで、nはデータセットの長さです。
入力データに対する重み付け方法を選択します。
| 直接重み付け |
|
|---|---|
| 機械的 |
|
| 統計 |
|
分散除数d の計算を制御します。
| DF | 自由度
|
|---|---|
| N | 欠損していない観測値の数
|
| WDF | 重みのあるDFの合計
|
| WS | 重みの合計
|
| WVR | 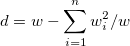 |
Q1、Q2、Q3を求める方法を決めます。
 番目のパーセンタイル(分位)をyとし、
番目のパーセンタイル(分位)をyとし、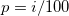 を設定します。そして、次のように定義します。
を設定します。そして、次のように定義します。
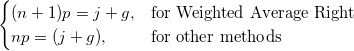
ここで、 j は、np, の整数部で、 g は、np の分数部であり、それぞれ異なる方法は 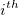 番目のパーセンタイル、 yを次に述べる方法で定義します。
番目のパーセンタイル、 yを次に述べる方法で定義します。
| 平均化による経験分布 | 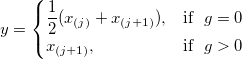 |
|---|---|
| 最近傍 | 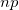 に最も近い番号の観測値 に最も近い番号の観測値
|
| 経験分布 | 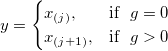 |
| 加重平均(右) | 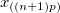 に向けた加重平均 に向けた加重平均
|
| 加重平均(左) | 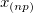 に向けた加重平均 に向けた加重平均
|
| Tukey Hinges | 以下のようにする。
すると、次のようになります。
|
|
Note: 重みが指定されていると、重み付けされたパーセンタイルが計算されます。p番目の重み付けされたパーセンタイル y は、平均を持つ経験分布関数 |
|
Origin 2022以降、グループ列の入力列のフォーマットは出力シート(例:DescStatsQuantities)で維持されます。たとえば、日時データの列に統計を実行する場合、出力シートでの列のフォーマットは自動で日時として設定されます(以前は、テキストとしてフォーマットされていました)。以前の動作に戻すには、@SCCSF = 0を設定します。システム変数の値を変更する方法については、FAQ-708 システム変数を永続的に変更するにはにあるシステム変数の変更を参照してください。 |
| グラフ | 結果のプロットの配置を制御します。
|
|---|---|
| データセット識別子 | 元のデータセットの識別子を選択します。
|
| レポート表 | レポートワークシート表の出力場所です。
|
| 値 | 値の出力先を指定します。
|
| オプショナルなレポートテーブル | レポートワークシートに出力する項目を指定します。
|
| ヒストグラム | 結果シートにヒストグラムを出力します。
ここにチェックを付けると、詳細の設定項目が表示されます。以下の項目があります。
|
|
|---|---|---|
| ボックスチャート | レポートシートにボックスチャートを出力します。入力データがグループ列を持つ場合、それに応じてボックスチャートもグループ化されます。グループ列がカテゴリーとして設定されていると、ボックスチャートは、グループ範囲に対するカテゴリータブ(列のプロパティ)で指定されたカテゴリー順を参照してプロットされます。 |