pkFind


目次

概要

様々な検索手法を使用してピークを検出します

追加の情報

この機能は8.0 SR5.で更新されています。詳細は、リリースノートを参照してください。

コマンドラインでの使用法

pkfind method:=first; // pick peaks by using the first derivative method.

Xファンクションの実行オプション

スクリプトからXファンクションにアクセスする場合、追加のオプションスイッチについてのページを参照してください。

変数

表示
名 		変数
名 		I/O
と
データ型 		デフォルト
値 		説明
入力 iy

入力

XYRange

<active>
 入力データを指定します。
スムージングポイント数 smooth

入力

int

0
 Savitzky-Golayスムージングは、ピーク検出前にスペクトルデータに実行することができます。スムージングを実行する場合、この変数を使ってSavitzky-Golayスムージングの移動ウィンドウでのポイント数(正の整数)を入力します。スムージングを実行したくない場合、この変数を0にセットします。
方向 dir

入力

int

b
 ピークの方向を指定します。

オプションリスト：

  • p：正
正のピークのみを検出
  • n：負
負のピークのみを検出
  • b：両方
正負両方のピークを検出
手法 method

入力

int

max
 ピークを検索するのに使用する手法を指定します。

オプションリスト：

  • max：局所最大
局所最大法を使ってピークを探します。
  • win:：ウィンドウサーチ
ウィンドウサーチ法を使ってピークを探します。
  • first:一次微分
一次微分法を使ってピークを探します。
  • second:2次微分(隠れたピークを探す)
2次微分法を使ってピークを探します。この方法は、データ内の隠れたピークを検出することができます。
  • residue:1次微分後の残差 (隠れたピークを探す)
1次微分法後の残差を使ってピークを探します。この方法は、データ内の隠れたピークを検出することができます。
局所ポイント数 npts

入力

int

20
 これは、手法の変数が0 (max)の場合のみ利用できます。局所的な領域でのポイント数を指定します。これは局所最大法でピークを検索するのみ使用します。
サイズオプション option

入力

int

p
 これは、手法の変数が1 (win)の場合のみ利用できます。これは、高さと幅の変数(下記)がどのように解釈するかを指定します。

オプションリスト：

  • r：素データのサイズ
値は元データのサイズとして解釈されます。
  • p：素データのパーセント
値は、入力データの合計の幅または最大高さのパーセントとして解釈されます。
高さ height

入力

double

20
 これは、手法の変数が1 (win)の場合のみ利用できます。これは矩形の高さを指定します。これはピークを検索するのに使用されます。
幅 width

入力

double

50
 これは、手法の変数が1 (win)の場合のみ利用できます。これは矩形の幅を指定します。これはピークを検索するのに使用されます。
ピークのフィルタリング filter

入力

int

h
 見つけるピークの数またはピークの高さに制限をつけるかどうかを指定します。

オプションリスト：

  • 0=none:なし
見つかったピークの数やピークの高さに制限を付けません。
  • 1=h:高さ
下の 値 変数と一緒に動作します。変数の値より大きい高さのピークを探します。
  • 2=num:個数
下の 値 変数と一緒に動作します。ピークの数は変数の値より少なくなります。
  • 3=hp:高さ %
下の 値 変数と一緒に動作します。変数の値より大きい高さのパーセントを探します。
値 しきい値高さ / ピークの数 / しきい値高さ(%)

入力

double

0
 この変数は、上の filter 変数と一緒に動作します。見つかったピークの最小高さ、または見つかったピークの最大数、または見つかったピークの高さパーセントを指定します。
最大半幅 hwidth

入力

double

0
 ピークマーカを探す最大の範囲を指定します。
ピーク裾の高さ fheight

入力

double

0
 ピークマーカを探す高さのしきい値を指定します。
ピーク中央のインデックス ocenter

出力

ベクター

<入力>!(<新規>)
 デフォルトでピーク中心のインデックスを出力します。ピーク中心のインデックスを出力する場所を指定します。
左マーカのインデックス oleft

出力

ベクター

<入力>!(<新規>)
 左ピークマーカのインデックスを出力するかどうかを指定します。
右マーカのインデックス oright

出力

ベクター

<input>!(<new>)
 右ピークマーカのインデックスを出力するかどうかを指定します。
ピークの中心のX値 ocenter_x

出力

ベクター

<入力>!(<新規>)
 ピークの中心のX値を出力するかどうかを指定します。
ピークの中心のY値 ocenter_y

出力

ベクター

<入力>!(<新規>)
 ピークの中心のY値を出力するかどうかを指定します。
左マーカーのX値 oleft_x

出力

ベクター

<入力>!(<新規>)
 左マーカーのX値を出力するかどうかを指定します。
左マーカーのY値 oleft_y

出力

ベクター

<入力>!(<新規>)
 左マーカーのY値を出力するかどうかを指定します。
右マーカーのX値 oright_x

出力

ベクター

<入力>!(<新規>)
 右マーカーのX値を出力するかどうかを指定します。
右マーカーのY値 oright_y

出力

ベクター

<入力>!(<新規>)
 右マーカーのY値を出力するかどうかを指定します。

説明

このXファンクションは、さまざまな方法でピーク(ピークの中心とピークマーカ)を見つけ、ピーク中心のインデックスを出力するのに使用できます。

サンプル

/* このサンプルでは、スペクトルデータのピークを決定する方法を示します。
\Samples\Spectroscopy フォルダのサンプルデータを使用します。
1.Originのブックにサンプルデータをインポート
2.Xファンクションpkfindでピークを検索
3.元のデータと見つかったピークをプロット
*/ //7つのピークがあるスペクトルデータをインポート string fname$=system.path.program$ + "Samples\Spectroscopy\HiddenPeaks.dat"; newbook sheet:=0; newsheet cols:=5 labels:="Time|Spectrum Data|Peak Center Indices|Peak Center X|Peak Center Y"; impASC; string bkn$=%H; //ピーク中心を検索 pkFind iy:=col(2) method:=second ocenter:=col(3) oleft:=<none> oright:=<none> ; //ピーク中心をインデックスで検索 col(4)=col(1)[col(3)];	//X位置 col(5)=col(2)[col(3)];	//Y位置 //黒線でスペクトルデータをプロット plotxy iy:=col(2) plot:=200; //ピーク中心を赤の散布図でプロット plotxy iy:=[bkn$]1!(4,5) plot:=201  legend:=1 color:=2 ogl:=1!;

アルゴリズム

基本コンセプト

このXファンクションは、5つの手法でピークを探します。普通のピークは、局所最大、ウィンドウサーチ、1次微分の手法で簡単に見つけることができます。データに隠れたピークが含まれる場合、別の手法、2次微分や1次微分後の残差を使います。

Pkfind help English files image004.jpg

局所最大法

ピーク検出は、極値(極大値や極小値)に基づいて行われます。手順は以下の通りです。

  1. 入力曲線上のすべてのポイントについて、Originは、範囲内のポイント間の極値（最大または最小）であるかどうかをチェックします。このポイントは、このポイントを中心とし、左側と右側の両方から局所ポイント数の長さを持ちます。ポイントが極値の場合、候補となるピークの中心として、この点に印が付けられます。
    PkFind localmax.png
  2. 候補となるすべてのピークに対して、Originはピークのフィルタリングで指定した制約条件に合致するかチェックします。ピークフィルタを高さに設定し、しきい値高さを20にすると、高さが参照値の20％未満のピークは除外されます。
    参照値は下記の方法で決定されます： まず、スペクトルの最大値と最小値を取得します。ベースラインがスペクトルから差し引かれている場合、ベースライン減算後のスペクトルが使用されます。そして、最小値と最大値の絶対値を比較します。大きい方が、しきい値高さの参照値と見なされます。
  3. データポイントが候補ピークであり、ピークフィルタリングで指定された制約を満たしている場合、この候補ピークは実際のピークと見なされ、結果に出力されます。

ウィンドウサーチ法

このXファンクションは、移動矩形を使ってピークを検出します。この矩形はX軸に平行な2つの辺とY軸に平行な別の2つの辺を持ちます。次の4つのステップを実行し、正のピークが存在するかどうかを見つけます。

1. 矩形の左下のx座標をx1、右下のx座標をx2とします。入力曲線上にx値がx1であるようなポイントP1 (x1, y1) を見つけ、 また、入力曲線上にx値がx2であるような別のポイント P2 (x2, y2) を見つけます。

2. y1 と y2 を比較して、2つのyのうちより大きい方を y'として取ります。

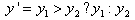
Pkfind rectangle 1.png

3. P1とP2の間の曲線の最大値yである曲線の局所最大値(yLocalMax)が見つかります。そして、局所最大値と y' の差を以下のように計算します。

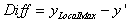
Pkfind rectangle 2.png

4. Diffを矩形の高さと比較します。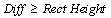Pkfind rectangle 411.pngの場合、局所最大値のポイントが正のピークだと見なされ、それ以外の場合、この矩形の中に正のピークは検出されません。

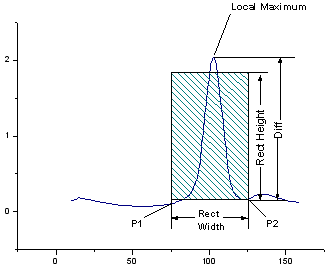
Pkfind rectangle 3.png

負のピークを見つける手順も同様です。

1. 矩形の左下のx座標をx1、右下のx座標をx2とします。入力曲線上にx値がx1であるようなポイントQ1 (x1, y1) を見つけ、 また、入力曲線上にx値がx2であるような別のポイント Q2 (x2, y2) を見つけます。

2. y1 と y2 を比較して、2つのyのうちより小さい方を y'として取ります。

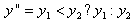
Pkfind rectangle 11.png

3. Q1とQ2の間の曲線の最小値yである曲線の局所最小値(yLocalMin)が見つかります。そして、局所最小値と y' の差を以下のように計算します。

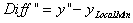
Pkfind rectangle 21.png

4. Diff"を矩形の高さと比較します。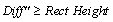Pkfind rectangle 410.pngの場合、局所最小値のポイントが負のピークだと見なされ、それ以外の場合、この矩形の中に負のピークは検出されません。

これらのステップが終了したら、矩形が1ポイント右に動き、矩形がデータ範囲外に出るまで、これらのステップを繰り返し実行します。

一階微分法

基本的な考え方は以下の通りです。1) 正のピークの中心が 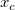x_c にあるとき、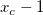x_c-1 での一階微分は正になりますが、 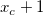x_c+1での一階微分は負になります。2) 負のピークの中心が 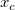x_cにあるとき、 -1 での一階微分は負になりますが、 +1 での一階微分は正になります。

二階微分法

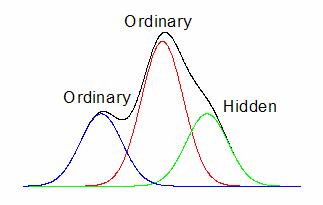
データの滑らかな2階微分は、元データの極値を検出でき、これは通常のピークと隠れピークの両方のピーク位置に対応します。

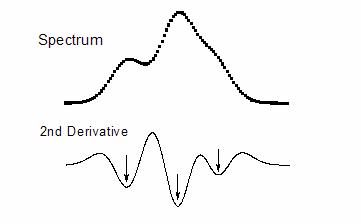
Pkfind help English files image006.jpg

図ではスペクトルデータは2つの局所最大ピークと1つの隠れたピークで構成されています。その2階微分曲線が下側に表示され、極小値により、この中に隠れたピークがあることがわかります。

一階微分後の残差

基本的な考え方は以下の通りです。

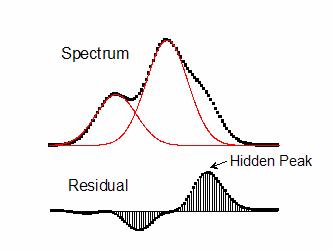
1.一階微分法を使ってピークを検出し、個々にピークをフィットします。 そして、各ピークのフィット曲線を累積します。

2.スペクトルデータと累積フィットデータ間の残差を計算します。

3.それぞれ対応するデータポイントの残差は隠れたピークとして考えられるしきい値より大きくなります。

以下は、隠れたピークを見つける一階微分法の例です。このスペクトルデータには2つの正のピークと1つの隠れたピークがあります。2つの正のピークのフィット曲線の累積データがスペクトルデータから減算されると、隠れたピークが残差プロット内にはっきりと現れます。

Pkfind help English files image008.jpg

参考文献

関連するXファンクション

blauto, fitpeaks, pa, PaMultiY, NLfitpeaks

キーワードスペクトル、二次微分、局所最大、ウィンドウ、しきい値