2.12.6 pkFind


Contents

Brief Information

Find peaks using various search methods

Additional Information

This feature is updated in 8.0 SR5. For more details, please refer to Release Notes.

Command Line Usage

pkfind method:=first; // pick peaks by using the first derivative method.

X-Function Execution Options

Please refer to the page for additional option switches when accessing the x-function from script

Variables

Display
Name 		Variable
Name 		I/O
and
Type 		Default
Value 		Description
Input iy

Input

XYRange

<active>
 Specify the input data.
Smooth Points smooth

Input

int

0
 Savitzky-Golay smoothing can be performed to the spectrum data before the peak finding. If you want to perform the smoothing, specify the desired number of points (a positive integer) in the moving window for the Savitzky-Golay smoothing with this variable. If you do not want to perform the smoothing, set this variable to 0.
Direction dir

Input

int

b
 Specify the direction of the peaks.

Option list:

  • p:Positive
Only pick positive peaks
  • n:Negative
Only pick negative peaks
  • b:Both
Pick both positive and negative peaks
Method method

Input

int

max
 Specify the method used to find the peaks.

Option list:

  • max:Local Maximum
Use the Local Maximum method to find the peaks.
  • win:Window Search
Use the Window Search method to find the peaks.
  • first:1st Derivative
Use the first derivative method to find the peaks.
  • second:2nd Derivative (search Hidden peaks)
Use the second derivative method to find the peaks. This method is capable of detecting hidden peaks in the data.
  • residue:Residual after 1st Derivative (search Hidden peaks)
Use the Residual after 1st Derivative method to find the peaks. This method is capable of detecting hidden peaks in the data.
Local Points npts

Input

int

20
 This is available only when the method variable is 0 (max). It specifies the number of points in the local area, which will be used for finding the peaks with the Local Maximum method.
Size Option option

Input

int

p
 This is available only when the method variable is 1 (win). It specifies how the values for the height and width variable (see below) are interpreted.

Option list:

  • r:Raw Size
The values will be interpreted as raw sizes.
  • p:Percent of Raw Data
The values will be interpreted as the percentages with respect to the total width or maximum height of the input data.
Height height

Input

double

20
 This is available only when the method variable is 1 (win). It specifies the height of the rectangle, which is used to find the peaks.
Width width

Input

double

50
 This is available only when the method variable is 1 (win). It specifies the width of the rectangle, which is used to find the peaks.
Filter Peaks by filter

Input

int

h
 Specify whether you want to limit the number of found peaks or the height of the peaks.

Option list:

  • 0=none:None
Neither the number of found peaks nor the heights of the peaks are limited.
  • 1=h:Height Value
This works with the Value variable below. The heights value of the found peaks will not be less than the value of that variable
  • 2=num:Number
This works with the Value variable below. The number of found peaks will not excess the value of that variable.
  • 3=hp:Height %
This works with the Value variable below. The height percent of the found peaks will not be less than the value of that variable
Threshold Height / Number of Peaks / Threshold Height(%) value

Input

double

0
 This variable works with the filter variable above. It specifies the minimum height of the found peaks / the maximum number of the found peaks/ height percent of the found peaks
Maximum Half Width hwidth

Input

double

0
 Specify the maximum range for searching the peak markers.
Foot Height fheight

Input

double

0
 Specify the threshold height for searching the peak markers.
Center Peaks Indices ocenter

Output

vector

<input>!(<new>)
 Output the the indices of peak centers by default. Specify where to output the indices of peak centers.
Left Markers Indices oleft

Output

vector

<input>!(<new>)
 Specify whether to output the indeces of the left peak markers.
Right Markers Indices oright

Output

vector

<input>!(<new>)
 Specify whether to output the indeces of the right peak markers.
Xs of Peak Centers ocenter_x

Output

vector

<input>!(<new>)
 Specify whether to output the X values of the peak centers.
Ys of Peak Centers ocenter_y

Output

vector

<input>!(<new>)
 Specify whether to output the Y values of the peak centers.
Xs of Left Markers oleft_x

Output

vector

<input>!(<new>)
 Specify whether to output the X values of the left markers.
Ys of Left Markers oleft_y

Output

vector

<input>!(<new>)
 Specify whether to output the Y values of left markers.
Xs of Right Markers oright_x

Output

vector

<input>!(<new>)
 Specify whether to output the X values of the right markers.
Ys of Right Markers oright_y

Output

vector

<input>!(<new>)
 Specify whether to output the Y values of the right markers.

Description

This X-Function can be used to find peaks (peak centers and peak markers) with various methods and output the indices of peak centers .

Examples

/*
This example shows you how to detect peaks in spectrum data.
The sample data used is in
  \Samples\Spectroscopy folder.
1. Import the sample data into a book in Origin.
2. Use the pkfind X-Function to locate the peaks.
3. Plot the original data and the found peaks.
*/
//Import spectrum data with 7 peaks
string fname$=system.path.program$ + "Samples\Spectroscopy\HiddenPeaks.dat";
newbook sheet:=0;
newsheet cols:=5 labels:="Time|Spectrum Data|Peak Center Indices|Peak Center X|Peak Center Y";
impASC;
string bkn$=%H;

//Find peak centers
pkFind iy:=col(2) method:=second ocenter:=col(3) oleft:=<none> oright:=<none> ;

//Find peak center positions by their indeces
col(4)=col(1)[col(3)];	//X positions
col(5)=col(2)[col(3)];	//Y positions
//Plot spetrum data as a black line
plotxy iy:=col(2) plot:=200;
//Plot peak centers as red scatters
plotxy iy:=[bkn$]1!(4,5) plot:=201  legend:=1 color:=2 ogl:=1!;

Algorithm

Basic Concept:

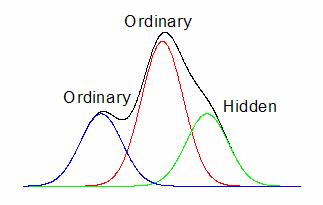
This X-Function provides 5 methods to find peaks. Usually, ordinary peaks can be easily found by the Local Maximum, Window Search and First Derivative methods. If your data contains hidden peaks, more sophisticated methods like Second Derivative method and Residual after First Derivative method should be used.

Pkfind help English files image004.jpg

Local Maximum Method

The peak finding is based on local extrema (maximum or minimum). The steps are as follows:

  1. For every point on the input curve, Origin checks whether it is the extrema (maximum or minimum) among points in the range, which centers in this point and has a length of Local Points from both the left and the right sides. If it is the extrema, this point will be marked as the center of a candidate peak.
    PkFind localmax.png
  2. If a data point is candidate peak, Origin will further check whether it meets the constraints specified in Peak Filtering option. If Filter Method is set to By Height and Threshold Height (%) to 20, the peaks whose heights are less than 20% of the reference value will be filtered out.
    The reference value is determined in the following way: First, get the maximum and the minimum value of the spectrum. If a baseline has been subtracted from the spectrum, the spectrum after baseline subtraction is used. Then compare the absolute values of the max value and the min value. The greater one will be regarded as the reference value of the Threshold Height.
  3. If a data point is candidate peak and meets the constraints specified in the Peak Filtering, this candidate peak will be considered a real peak and will be outputted in the result.

Window Search Method

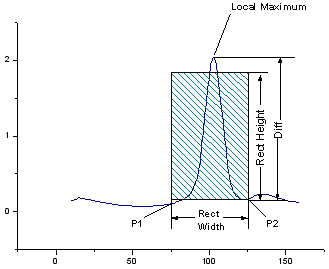
This X-Function picks the peaks with a moving rectangle, which has two sides paralleled to the X axis and the other two sides paralleled to the Y axis. The following four steps are performed so as to find whether a positive peak exists:

1.Suppose the x coordinate of the bottom-left corner of the rectangle is x1, and the x coordinate of its bottom-right corner of the rectangle is x2. We find a point P1 (x1, y1) on the input curve, whose x value is x1, and another point P2 (x2, y2) on the curve, whose x value is x2.

2.We compare y1 and y2 and take the larger of the two as y':

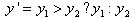
Pkfind rectangle 1.png

3.The local maximum of the curve (yLocalMax), which is the maximum y value on the curve between P1 and P2, is found. Then, we compute the difference between the local maximum and y' as follows:

Pkfind rectangle 2.png

4.Compare Diff with the rectangle height. If 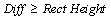Pkfind rectangle 411.png , the local maximum point will be regarded as a positive peak; otherwise, no positive peaks will be picked within this rectangle.

Pkfind rectangle 3.png

The procedure for finding a negative peak is similar:

1.Suppose the x coordinate of the bottom-left corner of the rectangle is x1, and the x coordinate of its bottom-right corner of the rectangle is x2. We find a point Q1 (x1, y1) on the input curve, whose x value is x1, and another point Q2 (x2, y2) on the curve, whose x value is x2.

2.We compare y1 and y2 and take the lesser of the two as y":

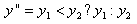
Pkfind rectangle 11.png

3.The local minimum of the curve (yLocalMin), which is the minimum y value on the curve between Q1 and Q2, is found. Then, we compute the difference between the local minimum and y" as follows:

Pkfind rectangle 21.png

4.Compare Diff" with the rectangle height. If 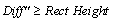Pkfind rectangle 410.png, the local minimum point will be regarded as a negative peak; otherwise, no negative peaks will be picked within this rectangle.

After these steps are completed, the rectangle will be moved 1 point toward the right and these steps are performed again, until the rectangle is out of the data range.

First Derivative Method

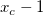The basic idea of this method is as follows: 1) A positive peak center locates in a position x_c, where the first derivative at x_c-1 is positive while the first derivative at x_c+1 is negative; 2) A negative peak center locates in a position x_c, where the first derivative at -1 is negative while the first derivative at +1 is positive.

Second Derivative Method

The smoothed second derivative of the data is capable of detecting local extrema in the raw data, which corresponds to peak positions of both ordinary and hidden peaks.

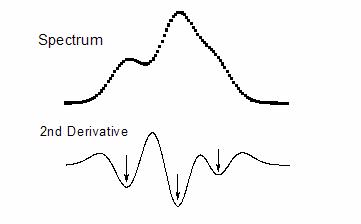
Pkfind help English files image006.jpg

In the figure, the spectrum consists of two local maxima peaks and one hidden peaks. Its second derivative curve is shown in the lower plot, in which the hidden peak is revealed by the local minima.

Residual after 1st Derivative

The basic ideal is as follows:

1. Use the First Derivative method to find peaks and fit the peaks individually. Then cumulate the fitting curves of every peak.

2. Calculate the residuals between the spectrum data and the cumulated fitting data.

3. The points whose corresponding residuals are greater than a threshold will be considered as hidden peaks.

Following is an example using Residual after First Derivative method to find hidden peaks. The spectrum contains two positive peaks and one hidden peak. When the cumulated data of the fitting curves of the two positive peaks are subtracted from the spectrum, the hidden peak is clearly revealed in its residual plot.

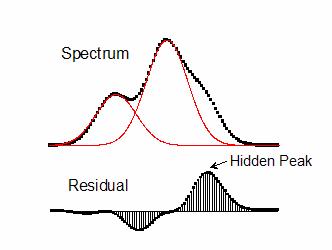
Pkfind help English files image008.jpg

References

Related X-Functions

blauto, fitpeaks, pa, PaMultiY, NLfitpeaks

Keywords:spectrum, second derivative, local maximum, window, threshold