nag_opt_handle_init (e04rac) : NAG Library, Mark 26

nag_opt_handle_init (e04rac) initializes an empty problem with

n

decision variables,

x

The handle can store various problem formulations, including linear programming (LP)

\begin{array}{l} \underset{x \in ℝ^{n}}{minimize} & c^{T} x & (a) \\ subject to & l_{B} \leq B x \leq u_{B} & (b) \\ l_{x} \leq x \leq u_{x}, & (c) \end{array}

(1)

quadratic programming (QP)

\begin{array}{l} \underset{x \in ℝ^{n}}{minimize} & \frac{1}{2} x^{T} H x + c^{T} x & (a) \\ subject to & l_{B} \leq B x \leq u_{B} & (b) \\ l_{x} \leq x \leq u_{x}, & (c) \end{array}

(2)

nonlinear programming (NLP)

\begin{array}{l} \underset{x \in ℝ^{n}}{minimize} & f (x) & (a) \\ subject to & l_{g} \leq g (x) \leq u_{g} & (b) \\ l_{B} \leq B x \leq u_{B} & (c) \\ l_{x} \leq x \leq u_{x} & (d) \end{array}

(3)

least squares (LSQ) problems

\begin{array}{l} \underset{x \in ℝ^{n}}{minimize} & \sum_{i = 1}^{m_{r}} {r_{i} (x)}^{2} & (a) \\ subject to & l_{x} \leq x \leq u_{x}, & (b) \end{array}

(4)

linear semidefinite programming (SDP)

\begin{array}{l} \underset{x \in ℝ^{n}}{minimize} & c^{T} x & (a) \\ subject to & \sum_{i = 1}^{n} x_{i} A_{i}^{k} - A_{0}^{k} ⪰ 0, k = 1, \dots, m_{A} & (b) \\ l_{B} \leq B x \leq u_{B} & (c) \\ l_{x} \leq x \leq u_{x} & (d) \end{array}

(5)

or semidefinite programming with bilinear matrix inequalities (BMI-SDP)

\begin{array}{l} \underset{x \in ℝ^{n}}{minimize} & \frac{1}{2} x^{T} H x + c^{T} x & (a) \\ subject to & \sum_{i,j = 1}^{n} x_{i} x_{j} Q_{i j}^{k} + \sum_{i = 1}^{n} x_{i} A_{i}^{k} - A_{0}^{k} ⪰ 0, k = 1, \dots, m_{A} & (b) \\ l_{B} \leq B x \leq u_{B} & (c) \\ l_{x} \leq x \leq u_{x}, & (d) \end{array}

(6)

where

H

A_{i}^{k}

and

Q_{i j}^{k}

denote symmetric matrices,

B

is a general rectangular matrix,

m_{A}

is the number of semidefinite constraints (matrix inequalities) and

c

l

and

u

are vectors. The expression

S ⪰ 0

stands for a constraint on eigenvalues of a symmetric matrix

S

, namely, all the eigenvalues should be non-negative, i.e., the matrix

S

should be positive semidefinite.

3.1

Life Cycle of the Handle

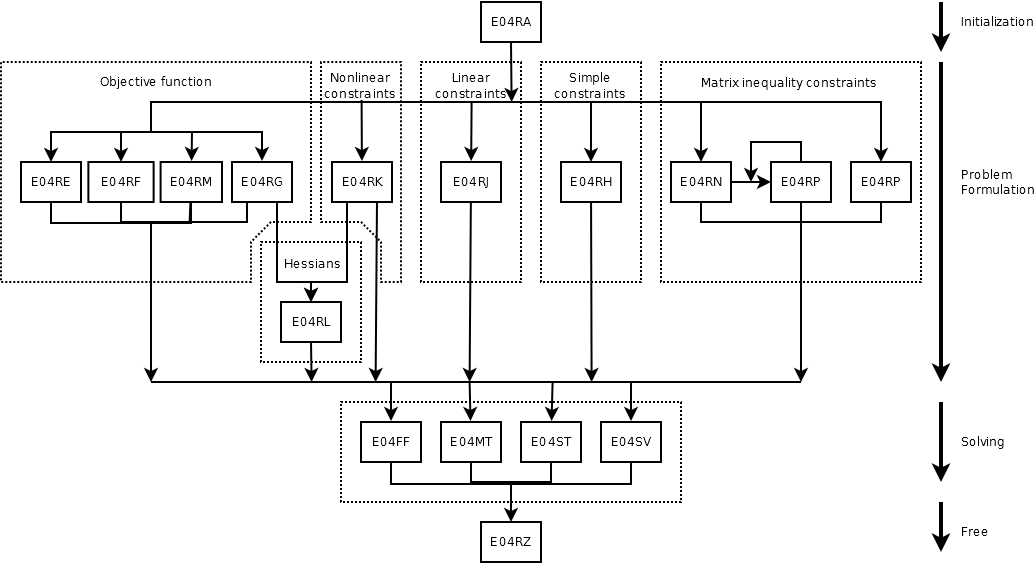
Each handle should pass four stages in its life as depicted in the diagram below. These are initialization, problem formulation, problem solution and deallocation. The initialization by nag_opt_handle_init (e04rac) and deallocation by nag_opt_handle_free (e04rzc) mark the beginning and the end of the life of the handle. During this time the handle must only be modified by the provided functions. Working with a handle which has not been properly initialized will result in

fail . code =

NE_HANDLE (uniform across the suite) and is potentially very dangerous as it may cause unpredictable behaviour.

After the handle has been initialized, various functions are provided to add the following basic building blocks to the problem formulation: objective function, simple variable bounds, (standard) linear and nonlinear constraints and matrix constraints. Some of these can be defined at most once (e.g., objective function) and an attempt to redefine them will return

fail . code =

NE_ALREADY_DEFINED. Others (matrix constraints) may be composed using several repetitive calls. The functions work in tight cooperation and if the provided data is not compatible with the previous information,

fail . code =

NE_REF_MATCH is returned.

The handle may be passed to one of the following functions to define the objective function:

nag_opt_handle_set_linobj (e04rec) – a linear objective (such as (1)(a) or (5)(a)) as a dense vector;
nag_opt_handle_set_quadobj (e04rfc) – a quadratic objective or a spare linear objective, such as (1)(a) or (2)(a);
nag_opt_handle_set_nlnobj (e04rgc) – a nonlinear objective function (3)(a);
nag_opt_handle_set_nlnls (e04rmc) – a nonlinear least squares objective function (4)(a).

Only one objective may be defined. If none of them are used the problem will find a feasible point satisfying the constraints.

The functions for constraint definition are:

nag_opt_handle_set_simplebounds (e04rhc) – simple bounds (box constraints), such as (1)(c) or (2)(c);
nag_opt_handle_set_linconstr (e04rjc) – linear constraints, such as (1)(b) or (2)(b);
nag_opt_handle_set_nlnconstr (e04rkc) – nonlinear constraints (3)(b);
nag_opt_handle_set_nlnhess (e04rlc) – second derivatives for the objective and/or constraints;
nag_opt_handle_set_linmatineq (e04rnc) – linear matrix inequalities (5)(b) or the linear part of bilinear matrix inequalities (6)(b);
nag_opt_handle_set_quadmatineq (e04rpc) – quadratic terms for bilinear matrix inequalities in (6)(b).

These functions may be called in an arbitrary order, however, a call to nag_opt_handle_set_linmatineq (e04rnc) must precede a call to nag_opt_handle_set_quadmatineq (e04rpc) for the matrix inequalities with bilinear terms and the nonlinear objective or constraints (nag_opt_handle_set_nlnobj (e04rgc) or nag_opt_handle_set_nlnconstr (e04rkc)) must precede the definition of the second derivatives by nag_opt_handle_set_nlnhess (e04rlc). A call to nag_opt_handle_set_linmatineq (e04rnc) can be repeated several times if more matrix inequality constraints are required.

When the problem is fully formulated, the handle can be passed to a solver which is compatible with the defined problem. The NAG optimization modelling suite comprises of nag_opt_handle_solve_dfls (e04ffc), nag_opt_handle_solve_lp_ipm (e04mtc), nag_opt_handle_solve_ipopt (e04stc) and nag_opt_handle_solve_pennon (e04svc). If the solver cannot deal with the given problem,

fail . code =

NE_SETUP_ERROR is returned. Once the solver is called, no further modifications of the problem formulation are allowed and calling any of the functions defining the objective function or the constraints will return

fail . code =

NE_PHASE. The solver may be called repetitively, for example, with various optional parameters and/or starting points.

Any optional parameters may be set by a call to nag_opt_handle_opt_set (e04zmc) at any time between the initialization by nag_opt_handle_init (e04rac) and the call to the solver or after the solver returns. Several optional parameters can be modified at once by nag_opt_handle_opt_set_file (e04zpc) when an option file is used. The current value of the optional parameters may be retrieved by nag_opt_handle_opt_get (e04znc).

For further details, see the documentation of the individual functions and the solvers which also contain a description of all the optional parameters.

References

Arguments

Error Indicators and Warnings

Accuracy

Parallelism and Performance

nag_opt_handle_init (e04rac) is not threaded in any implementation.

Further Comments

Example

See examples associated with other functions in the suite:

–	the example in Section 10 in nag_opt_handle_solve_dfls (e04ffc) demonstrates how to use a DFO LSQ solver,
–	the example in Section 10 in nag_opt_handle_solve_lp_ipm (e04mtc) solves a small LP example using an LP IPM solver,
–	the example in Section 10 in nag_opt_sdp_read_sdpa (e04rdc) demonstrates how to use the SDPA file reader and how to solve linear semidefinite programming problems, including printing of the matrix Lagrangian multipliers,
–	the example in Section 10 in nag_opt_handle_set_quadobj (e04rfc) presents an alternative way to compute the nearest correlation matrix by means of nonlinear semidefinite programming,
–	a matrix completion problem (minimization of a rank of a partially unknown matrix) formulated as SDP is demonstrated in Section 10 in nag_opt_handle_set_simplebounds (e04rhc), the example also demonstrates the monitoring mode of the solver nag_opt_handle_solve_pennon (e04svc),
–	the example in Section 10 in nag_opt_handle_set_linconstr (e04rjc) solves LP/QP problems read in from an MPS file by nag_opt_miqp_mps_read (e04mxc),
–	an application for statistics, $E$ optimal design, solved as an SDP problem is shown in Section 10 in nag_opt_handle_set_linmatineq (e04rnc),
–	the example in Section 10 in nag_opt_handle_set_quadmatineq (e04rpc) reads a BMI-SDP problem from a file which can be modified, in this case it solves a Static Output Feedback (SOF) problem,
–	the example in Section 10 in nag_opt_handle_set_get_real (e04rxc) demonstrates how an approximate solution can be extracted during a monitoring step of nag_opt_handle_solve_lp_ipm (e04mtc),
–	the example in Section 10 in nag_opt_handle_print (e04ryc) walks through the life cycle of the handle in which a BMI-SDP problem is formulated and solved,
–	an example in Section 10 in nag_opt_handle_solve_ipopt (e04stc) is a small test from Hock and Schittkowski set to show how to call the NLP solver,
–	the simple example in Section 10 in nag_opt_handle_solve_pennon (e04svc) demonstrates on the Lovász $ϑ$ function eigenvalue optimization problem formulated as SDP.

NAG Library Function Document

nag_opt_handle_init (e04rac)

▸▿ Contents

1

Purpose

2

Specification

3

Description

3.1

Life Cycle of the Handle

4

References

5

Arguments

6

Error Indicators and Warnings

7

Accuracy

8

Parallelism and Performance

9

Further Comments

10

Example

NAG Library Function Document

nag_opt_handle_init (e04rac)

▸▿ Contents

1 Purpose

2 Specification

3 Description

3.1 Life Cycle of the Handle

4 References

5 Arguments

6 Error Indicators and Warnings

7 Accuracy

8 Parallelism and Performance

9 Further Comments

10 Example