stft

内容

1 メニュー情報
2 概要
3 追加の情報
4 コマンドラインでの使用法
5 変数
6 サンプル
7 アルゴリズム
8 詳細な情報
9 関連のXファンクション

メニュー情報

解析：信号処理： STFT

概要

短時間フーリエ変換を実行します。

追加の情報

これはOriginProのみの機能です。

コマンドラインでの使用法

1. stft ix:=col(2);

2. stft ix:=col(2) interval:=4;

3. stft ix:=col(2) option:=complex;

4. stft ix:=col(2) winlen:=32 fftlen:=64 overlap:=16;

5. stft ix:=col(2) win:=tri;

6. stft ix:=col(2) win:=gauss alpha:=3;

7. stft ix:=col(2) win:=kaiser beta:=2;

8. stft ix:=col(2) plot:=0;

変数

表示名	変数名	I/O とデータ型	デフォルト値	説明
入力	ix	入力 vector<complex>	<active>	入力信号を指定します。
指定する	mode	入力 int	0	オプションリスト: interval:間隔 {0} freq:周波数 {1}
サンプリング間隔	interval	入力 double	<自動>	modeがinterval(間隔)の場合、サンプリング間隔を指定します。デフォルトは <自動>で、これは自動に計算される間隔に対応しています。
サンプリング周波数	freq	入力 double	<自動>	modeがfrequency(周波数)の場合、サンプリング間隔を指定します。デフォルトは <自動>で、これは自動に計算される周波数に対応しています。
FFT長	fftlen	入力 int	256	FFT区間の大きさを指定します。
ウィンドウ長	winlen	入力 int	256	ウィンドウの大きさを指定します。これはFFT区間の大きさより大きくてはいけません。
オーバーラップ	overlap	入力 int	128	ウィンドウ区間が重なるデータポイントの数を指定します。ウィンドウの大きさより小さくしてください。
ウィンドウ法	win	入力 int	4	FFTで使用するウィンドウ法を指定します。オプションリスト: rect:矩形 {0} 矩形ウィンドウ welch:Welch {1} Welchウィンドウ tri:Triangular {2} Triangularウィンドウ bartlett:Bartlett {3} Bartlettウィンドウ hanning:Hanning {4} Hanningウィンドウ hamming:Hamming {5} Hammingウィンドウ blackman:Blackman {6} Blackmanウィンドウ gauss:Gaussian {7} Gaussianウィンドウ kaiser:Kaiser {8} Kaiserウィンドウ
アルファ値	alpha	入力 double	0	ウィンドウ法がGaussianの場合のみ利用できます。ガウスウィンドウに対して、アルファパラメータを指定します。
ベータ値	beta	入力 double	0	ウィンドウ法がKaiserの場合のみ利用できます。Kaiserウィンドウに対して、ベータパラメータを指定します。
オプション	option	入力 int	2	計算オプションを指定します。デフォルト値は2で、これはdB単位での振幅の計算に対応しています。オプションリスト: complex:Complex Result {0} STFTの複素数の結果が計算されます。 amp:Amplitude Result {1} 複素数の結果の振幅が与えられます。 ampdb:Amplitude in dB {2} dB単位での振幅が計算されます。
時間と周波数の入れ替え	swapxy	入力 int	0	イメージプロットの時間軸と周波数軸を入れ替えるかどうかを指定します。
出力行列	om	出力 MatrixObject	[<新規>]<新規>!	出力する行列を指定します。
プロット	plot	入力 int	1	結果のイメージプロットを生成するかどうかを指定します。
出力ワークシート	rd	出力 ReportData	[<入力>]<新規>	出力ワークシートの指定をします。

サンプル

1.デフォルトの設定で、列Bに対してSTFTを実行します。

stft ix:=col(b)

2.Hanning法でSTFTを実行するには

stft -d

ダイアログボックスを開きます。そしてウィンドウの種類で、Hanningウィンドウを選択します。

3.事前に保存したMyThemeという分析テーマを使ってSTFTを実行するには、コマンドウィンドウに次のように入力します。

stft -t "MyTheme"

アルゴリズム

STFTの計算

STFTは、次の手順で計算します。

1.Nポイントが入力信号から取られます。Nはウィンドウサイズです。

2.選択したウィンドウの種類を使って、抽出したデータをポイント毎に掛け算します。

3.ウィンドウサイズがFFT区間のサイズより小さい場合、ウィンドウの両側にゼロが付加されます。

4.FFTは、FFT区間で計算されます。

5.ユーザが指定した重なりサイズに従ってウィンドウを移動し、入力信号の終わりまでステップ1からステップ4を繰り返します。

ウィンドウ関数

ウィンドウの移動は次のように定義されます。

矩形ウィンドウ：

Welchウィンドウ：

Triangularウィンドウ：

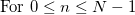
$\mbox{For } 0 \le n \le N-1$

$w[n]= \begin{cases} \frac{2}{N+1}(\frac{N+1}{2}-|n-\frac{N-1}{2}|), & \mbox{if }N\mbox{ is odd} \\ \frac{2}{N}(\frac{N}{2}-|n-\frac{N-1}{2}|), & \mbox{if }N\mbox{ is even} \end{cases}$