関連する動画はこちら: 関連する動画はこちら:Analysis of Variance (ANOVA)
|
関連する動画はこちら: 関連する動画はこちら:Analysis of Variance (ANOVA) |
目次 |
要因分散分析は、実験の無作為配置を考慮します。
Originは以下の要因分散分析をサポートしています。
| デザイン | 詳細 |
|---|---|
| 一元配置 | 1つのっ要因で3つまたはそれ以上のレベルを比較します。 |
| 二元配置 | 2つの要因の複数れ別の影響を比較し、2変数間の相互作用の影響を分析するために使用されます。 |
| 三元配置(Proのみ) | 連続する従属変数の3つの独立変数の相互作用効果を検定します(つまり、三元の相互作用があります)。 |
分散分析に加え、Originには、平均比較、実際または仮説の検出力分析の様々な手法があります。
ANOVAモデルには次の仮定があります。
正規性の検定および等分散性の検定(Leveneの検定)が仮定の検証に使用できます。詳しくは仮定をご覧ください。
分散分析では、有効なオムニバスの検定結果を得てから複数の比較手法が使われています。有意なANOVAの結果は、グローバルな帰無仮説H0が棄却されることを示します。H0は、平均が比較されるグループ間で等しいという仮説になります。どの平均が異なっていたのかを見極めるのに複数比較を行います。
Originは平均比較を行う手法を8つ準備しています。それらは、Tukey, Bonferroni, Dunn-Sidak, Fisher LSD, Scheffe, Dunnett, Holm-Bonferroni, Holm-Sidakです。
| Tukey | Tukey法は全てのタイプIのエラーを制御します。Tukeyが使用されると、全ての信頼係数は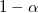 でサンプルサイズと等しく、つまり、タイプIのエラーのリスクはちょうど でサンプルサイズと等しく、つまり、タイプIのエラーのリスクはちょうど になります。サンプルサイズが等しくない場合、タイプIのエラーのリスクは になります。サンプルサイズが等しくない場合、タイプIのエラーのリスクは より低くなります。 より低くなります。 |
|---|---|
| Bonferroni | Bonferroni 法は全てのタイプIのエラーを制御し、Tukeyと比べて保守的です。この手法は、一般にペアワイズ比較検定に使用されます。 |
| Fisher's LSD | Fisher's LSD検定は、全てのタイプIのエラーを制御しません。そのため、この検定は、全体F検定が有意で、対象内の比較数値が小さい場合のみ使用してください。 |
| Scheffé | 比較数が小さい場合、Schefféはとても保守的(Bonferroni以上)です。Schefféは多くの比較と複数の比較がある場合、より強力な手法になります。複雑な複数比較が行われるときに使用します。 |
| Dunn-Sidak | 比較する数が大きい場合、Dunnett検定よりも強力です。 |
| Holm-Bonferroni | この手法は、Bonferroni手法よりも保守的ではなくより強力です。そのため、Bonferroni-Holm法では、帰無仮説を棄却する可能性が高くなります。 |
| Holm-Sidak | Holm検定よりも強力な手法です。しかし、信頼区間を算出することはできません。 |
検出力解析は、サンプルデータの実際の検出力の計算を行い、差を検出する可能性を知ることができます。追加のサンプルサイズが指定された場合に、仮定の検出力を計算する手助けになります。
データ範囲内の欠損値は、分析には含まれません。
Origin 2015から、グループ範囲内の欠損値と対応するデータ値は分析から除外されます。これ以前のバージョンでは、グループ範囲内の欠損値は、一つのグループとして扱われます。
| 特徴 | メニュー項目 |
|---|---|
| 一元配置 | 統計グラフ:ANOVA:一元配置の分散分析 |
| 二元配置 | 統計グラフ:ANOVA:二元配置の分散分析 |
| 三元配置(Proのみ) | 統計グラフ:ANOVA:三元配置の分散分析 |
|
このセクションで説明している項目
|