回帰は、最適なフィットを計算するために、よく使われます。回帰分析を実行する場合、モデルの回帰結果を表示している分析レポートシートを生成します。ここでは、回帰結果を簡単かつ素早く解釈する方法を説明します。
| Notes: これらの統計に関するアルゴリズムや公式については 非線形曲線フィットの理論をご参照ください。 |
フィット値は、以下のようにパラメータ表に表示されます。

データポイントに最も近い曲線を作成するフィットの各パラメータの推定値
パラメータの標準誤差からフィットパラメータの精度がどれぐらいなのか、検討がつきます。通常、標準誤差の大きさはフィット値よりも小さくなるはずです。標準誤差の値がフィットパラメータよりもとても大きい場合、フィッティングモデルは過剰パラメータである可能性があります。
回帰モデルの各項は有意でしょうか? または各予測変数は反応変数に寄与してますか? 係数のt検定により、このような疑問に対する回答を得ることができます。
パラメータの t検定に対する帰無仮説は、このパラメータが0であるということです。ですから、帰無仮説が棄却されると、対応する予測変数は有意性が無いと考えられ、それは反応変数に対する寄与が少ないことを示します。
また、 t検定は、検出ツールとして使うこともできます。例えば、多項式回帰で、t検定を使って、多項式モデルの適切な次数を調べることができます。t検定により、より高い次数の項は有意性が無いと判断できるまで、高い次数の項を追加していきます。
 で比較されます。(通常5%)t値が棄却値(
で比較されます。(通常5%)t値が棄却値(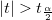 )よりも大きい場合は、有意差があるといえます。
)よりも大きい場合は、有意差があるといえます。 (通常は5%)の場合は、t検定のH0を除外する充分な根拠と考えられます。Prob>|t| が小さいほど、フィット値が0である確率は低いです。
(通常は5%)の場合は、t検定のH0を除外する充分な根拠と考えられます。Prob>|t| が小さいほど、フィット値が0である確率は低いです。UCLとLCLはそれぞれ信頼帯パラメータの上限と下限で、区間に真値がどれだけあるかを示します。例えば、上のパラメータ表図で、真値のオフセットとして95%確かなのは、4.16764 から 6.51631の区間、中央値(x0)の真値は、24.73246から 25.08134の区間、幅(w)の真値は 9.75801 から10.58138の区間です。
分散 - 共分散行列から計算される依存度の値は、通常、モデル内のパラメータの重要性を示します。たとえば、いくつかの依存度が1に近い場合、これらの間に相互依存関係がある可能性があります。言い換えると、関数は過剰パラメータ化されており、パラメータが過剰である可能性があります。意味のあるフィットモデルにするためには、このセクションを参照して制約を含める必要があります。
主な線形フィット統計値は、以下のように統計表に表示されます。
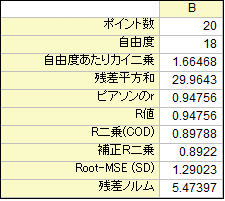
残差平方和は、通常RSSと略されます。各データポイントからフィット回帰直線までの垂直偏差の2乗の和です。RSSの値がゼロの場合、データが完全にフィットしていると推測できます。この統計値は、フィット線がデータによくフィットしているか判断する材料となります。一般的には、残差平方和が小さいほどモデルがデータによくフィットしていると言えます。
自由度あたりのカイ二乗値は、Scale Error with sqrtとも呼ばれ、残差平方和(RSS)を自由度で割ったものです。通常、自由度あたりカイ二乗値は、1に近いと良いフィット結果であることを示し、観測データとフィットデータの違いが誤差分散で一貫していることを示しています。誤差分散は、過大推定の場合、自由度あたりカイ二乗値は1より十分小さくなります。過小推定の誤差分散では、1より十分大きくなります。自由度あたりカイ二乗のフィット手順で正しい分散を選択する必要があることに注意が必要です。例えば、yデータが単純にスケール因子で掛け算されている場合、自由度あたりカイ二乗も同様にスケーリングされます。誤差分散を正しい係数でスケールする場合にのみ、自由度あたりカイ2乗の値が通常の値に戻ります。
ピアソンのrで示されるピアソンの相関係数は、対のデータ間の線形関係の強さを測定するのに役立ちます。ピアソンのrは、-1から1の値をとります。線形回帰では、正のピアソンのrの値は、予測変数(x)と応答変数(y)との間に正の線形相関があることを示し、負のピアソンのrの値は、および応答変数(y)を含むことを示します。ゼロの場合、データ間に線形相関がないことを表しています。さらに、値が-1または1に近いほど、より強い線形相関があることがわかります。
R二乗は、決定係数(COD)としても知られており、線形回帰を評価する統計手法です。これは、回帰直線によって説明される応答変数の変化のパーセンテージです。たとえば、R二乗は、モデルが応答変数のばらつきの約89%以上を説明していることを示します。従って、R二乗は常に0から1の間にあります。R二乗が0の場合は、フィット線がその平均値の周りの応答データのばらつきについて何も説明していないことを示します。 R二乗が1の場合、フィット線がその平均値周辺の応答データのすべてのばらつきを説明することを示します。一般的にR二乗値が大きいと、フィット直線がデータに良くフィットしていることになります。
R二乗はモデルがデータにどの程度良くフィットしているのかを評価し、R二乗は新しい予測因子が加わると常に大きくなります。より多くの予測変数を持つモデルがよりよく適合しているというのは誤っています。補正R二乗は、R二乗を修正したもので、フィット線の予測因子の数を調整したものです。つまり、予測因子が異なるフィット線を比較するために使用されます。予測因子の数が1より大きい場合、補正R二乗はR二乗より小さくなります。
|
フィット具合の評価については R二乗の追加情報をご覧ください。 |
回帰式がysのばらつきをどのように説明するかは、ANOVA表で以下のように表されます。
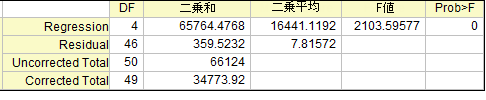
F値は、2つの平均平方の比であり、フィットモデルの平均平方を誤差の平均平方で除算することによって計算できます。例えば、上のモデルのF値は、65764.4768/16441.1192=2103.59577 となります。当てはめられたモデルが、傾きがゼロである、y = 定数と有意に異なるかどうか検定するための統計です。この比が1より大きくなればなるほど、フィットモデルはy = 定数と有意に異なるという証拠になります。
Prob>Fは、F検定のp値で、0から1の範囲の値の確率です。F検定のp値が、有意水準  (通常5%)より小さいと、フィットモデルがy =定数とは有意に異なると結論付けでき、フィットモデルが、傾きが0ではない非線形の曲線または線形であることと推測されます。
(通常5%)より小さいと、フィットモデルがy =定数とは有意に異なると結論付けでき、フィットモデルが、傾きが0ではない非線形の曲線または線形であることと推測されます。
| Note: 線形回帰では、ある値に切片を固定している場合、F検定のp値には意味が無く、切片一定としない線形回帰とは異なります。 |
変数間の関係は、以下に示すように、共分散と相関表で把握することができます。
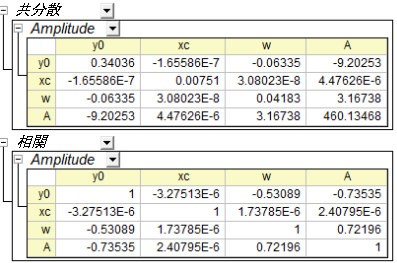
共分散値は、2つの変数間の相関を示し、回帰の共分散行列はすべてのパラメータの内部相関を表します。共分散行列の対角値は、パラメータの誤差の二乗に等しくなります。
相関行列は、 共分散値を再スケールして、その範囲を -1 から +1にします。+1 に近い値は、2つのパラメータが正の相関を持ち、 -1 に近い値は、2つのパラメータが負の相関を持つという意味になります。そして、0は2つのパラメータが全体的に独立していることを示しています。
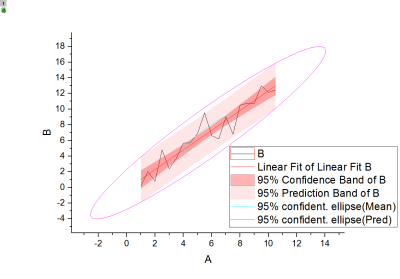
フィット曲線とその信頼帯、推定帯、楕円は、フィット曲線のグラフ上に以下のようにプロットされ、これは、フィットモデルをより直感的に解釈するのに役立ちます。
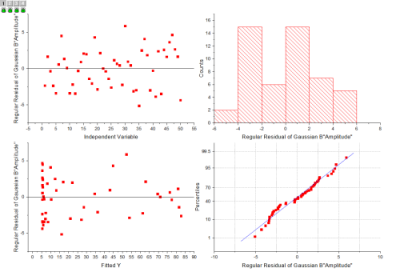
残差は次のように定義されます。
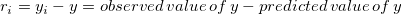
残差プロットを使用して回帰の質を評価することができます。これは、通常、レポートの最後に以下のように表示されます。