鋭いピークの関数を積分でフィットする

Fitting-Integral-SharpPeak

サマリー

このチュートリアルでは積分関数内に鋭いピークを持つ積分フィット関数を定義し、その関数でデータをフィットする方法を示します。

積分関数内に鋭いピークを含んでいるので、それを狭い間隔で積分する必要があります。そのため、このピークを3つの部分に区分けして積分を行います。

必要なOriginのバージョン:Origin 9.0 SR0

学習する項目

このチュートリアルでは、以下の項目について説明します。

• 積分フィット関数を定義する
• 鋭いピークの関数を積分する
• 積分の区間を複数に区分けする

サンプルとステップ

データのインポート

1. 新規ワークブックを作成します。
2. サンプルデータ の内容をワークブックにコピーします。
3. 列Bを選択し、作図：シンボル図：散布図と操作します。グラフは次のようになります。

フィット関数を定義する

フィットする積分関数は次の式で表されます。

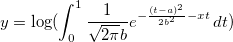
aとbはフィット関数内のパラメータです。

初期パラメータ値は、a=1e-4, b=1e-4となります。積分関数内には中心がaにあり、太さが2b程度のピークがあります。そして、ピークの幅(2e-4)は積分の範囲から見ても、とても狭いことが分かります。正しくピークの中心あたりで積分される事を確認するために、積分範囲である[0,1] は3つの区分に分けられています。[0,a-5*b], [a-5*b,a+5*b], [a+5*b,1].この区分内で積分が施され、最終的に合計します。

フィット関数ビルダーツールでフィット関数を定義します。

1. ツール：フィット関数ビルダーをメニューから選択します。
2. フィット関数ビルダーダイアログの処理のゴールページで進むのボタンをクリックします。
3. 関数名と関数形式のページでは関数カテゴリーの選択/新規名称のドロップダウンリストからUser Definedを選択します。次に関数名のエリアにfintpeakと入力し、関数形式で算術式を選びます。最後にフィット中に積分を実行のチェックを付けます。それから、進むボタンをクリックします。
4. 被積分関数ページでは被積分関数名の編集ボックス内にmyintと入力します。そして、被積分関数の変数の編集ボックスにはtを、引数の編集ボックスにはa, b, xを入力します。被積分関数ボックスに次のスクリプトを入力します。

   return 1/(sqrt(2*pi)*b)*exp(-(t-a)^2/(2*b^2)-x*t);
           
   

   それから、進むボタンをクリックします。

5. 変数とパラメータのページでは、パラメータエリアにa, bを入力します。進むボタンをクリックします。
6. 式形式の関数ページのパラメータタブでは、パラメータaとbの初期値を1e^-4に設定します。それから被積分関数タブをクリックし、下限と上側限界の値をそれぞれ0と1に設定し、a、b、xの値はそれぞれa、b、xと入力してください。
7. 式形式の関数ページで挿入ボタンをクリックします。クイックチェックのグループではｘ＝編集ボックスに0を入力し、評価ボタンをクリックします。すると、y=9.3e-21と表示されるはずです。ｘ＝０の時にｙは1へ近づかないといけないので、このピークが正しく積分されなかったことが分かります。積分を3つに区分し、関数内容ボックスに次のスクリプトを入力します。

   integral(myint, 0, a-5*b, a ,b ,x)+integral(myint, a-5*b, a+5*b, a ,b ,x)+
   integral(myint, a+5*b, 1, a ,b ,x)
           
   

   もう一度評価ボタンをクリックするとy=0.84が表示され、今回は正確にピークが積分されたことが分かります。

8. 式形式の関数ページの関数内容ボックスを次のスクリプトで更新します。

   log(integral(myint, 0, a-5*b, a ,b ,x)+integral(myint, a-5*b, a+5*b, a ,b ,x)
   +integral(myint, a+5*b, 1, a ,b ,x))
           
   

   完了ボタンをクリックします。

曲線をフィットする

1. 解析：フィット：非線形曲線フィットをメニューから選択します。NLFitダイアログで、設定タブを選択します。関数選択を選び、カテゴリドロップダウンリストからUser Definedを選びます。そして関数ドロップダウンリストではfintpeak関数を選びます。Note: 初期パラメータはフィット関数の定義中に設定されています。
2. フィットボタンをクリックし、フィットを行います。

フィット結果

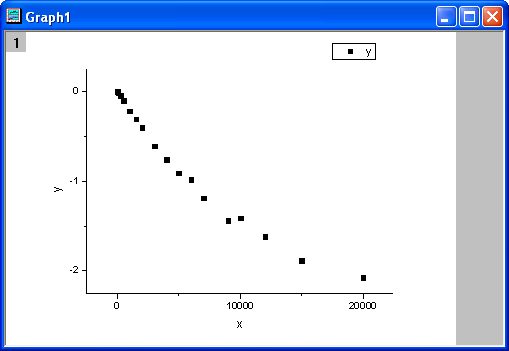
フィット曲線のグラフは次のようになります。

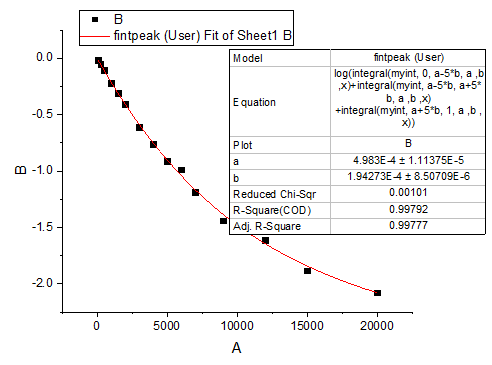
フィットパラメータは以下の通りです。

補正R二乗値は 0.99799です。つまり、このフィット結果はとても良いことを示しています。

サンプルデータ