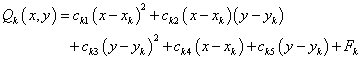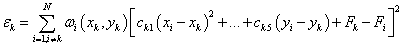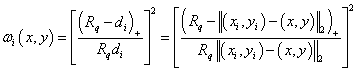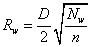2.2.1.9 xyz_shep_nag
Brief Information
Convert XYZ data to matrix using Modified Shepard gridding
Command Line Usage
1. xyz_shep_nag iz:=Col(3);
2. xyz_shep_nag iz:=Col(3) rows:=10 cols:=10;
4. xyz_shep_nag iz:=Col(3) q:=18 w:=9;
5. xyz_shep_nag iz:=Col(3) om:=[MBook]MSheet!Mat(1);
X-Function Execution Options
Please refer to the page for additional option switches when accessing the x-function from script
Variables
Display
Name
|
Variable
Name
|
I/O
and
Type
|
Default
Value
|
Description
|
| Input
|
iz
|
Input
XYZRange
|
<active>
|
Specifies the input XYZ range.
|
| Rows
|
rows
|
Input
int
|
20
|
Rows in the output matrix.
|
| Columns
|
cols
|
Input
int
|
20
|
Columns in the output matrix.
|
| Quadratic
|
q
|
Input
int
|
18
|
The quadratic interplant locality factor, which is used to calculate the influence radius of local approximate quadratic fitted function for each node. By default, q equals to 18. It is better to make q ≈ 2w and it should be satisfy that 0<w≤q. Modifying these factors could increase gridding accuracy, though note that the computation time can be greatly increased for large values (i.e. values that decrease the locality of the method.)
|
| Weight
|
w
|
Input
int
|
9
|
The weight function locality factor, which is used to calculate the weighting radius for each node. By default, w equals to 9. It is better to make q≈2w and it should be satisfy that 0<w<q. Modifying these factors could increase gridding accuracy, though note that the computation time can be greatly increased for large values (i.e. values that decrease the locality of the method.)
|
| Output Matrix
|
om
|
Output
MatrixObject
|
<new>
|
Specify the output matrix object.
See the syntax here.
|
Description
This function calls NAG library to perform modified Shepard gridding method which described by Franke and Nielson[1]. This is a distance-based method and improves the Shepard's method by some local strategies. During gridding, only the data points that lying within certain ranges, 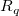 and
and  , to the grid nodes are considered. To make it easier for setting, two integers,
, to the grid nodes are considered. To make it easier for setting, two integers, 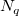 and
and 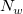 are used to calculate
are used to calculate 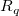 and
and  (parameters q and w of the function, and called Quadratic Interplant Locality Factor and Weight Function Locality Factor, respectively). Increase the value of
(parameters q and w of the function, and called Quadratic Interplant Locality Factor and Weight Function Locality Factor, respectively). Increase the value of 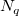 and
and 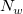 will make the calculation more global, vice versa. Generally speaking, setting
will make the calculation more global, vice versa. Generally speaking, setting 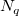 ≈
≈ 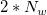 works fine and by default, Nq=18, Nw=9. However, the following constraints: 0<
works fine and by default, Nq=18, Nw=9. However, the following constraints: 0< 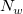 ≤
≤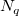 should be satisfied.
should be satisfied.
The value of 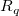 and
and  in this function is fixed and there is another similar X-Function xyz_shep which described by Renka[2] uses a vary
in this function is fixed and there is another similar X-Function xyz_shep which described by Renka[2] uses a vary 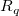 and
and  strategy.
strategy.
Examples
1. Import XYZ Random Gaussian.dat on the \Samples\Matrix Conversion and Gridding folder.
2. Type xyz_shep_nag 3 in the command window. Or type xyz_shep_nag -d to bring up the dialog.
Algorithm
This is a distance-based weighted gridding method which interpolate data by:
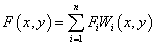 ,
,
where 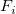 is the underlying function at nodes (
is the underlying function at nodes (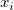 ,
, 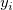 ), and
), and 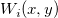 is the weights. To make the function more local,
is the weights. To make the function more local, 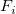 and
and 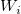 are calculated only by the data points lying in the circle with center (
are calculated only by the data points lying in the circle with center (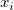 ,
, 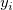 ) and some radius R..
) and some radius R..
Firstly, the weights are defined as:
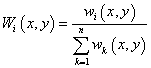 .
.
Given a radius  , the relative weight
, the relative weight 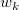 is:
is:
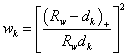 for
for
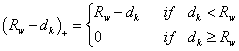 ,
,
and 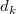 is the Euclidean distance between (x, y) and (
is the Euclidean distance between (x, y) and (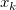 ,
, 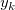 ):
):
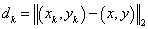 .
.
For any  >0, we have:
>0, we have:
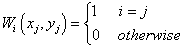
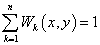 .
.
Secondly, the nodal function 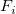 is replaced by a local approximation function
is replaced by a local approximation function 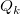 :
:
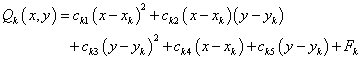
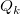 is the weighted least-square quadratic fitted function to the data located within
is the weighted least-square quadratic fitted function to the data located within 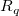 of nodal points. So the coefficients minimize:
of nodal points. So the coefficients minimize:
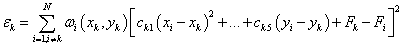
for
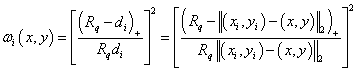 .
.
It can be seen above that the interpolate function is a local approximation function and depends on the radius of influence about nodal points, 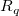 and
and  . In this method, two integers
. In this method, two integers 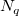 and
and 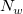 are used to calculate
are used to calculate 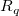 and
and  :
:
 and
and 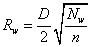 ,
,
where n is the number of data points and D is the maximum distance between any pair of data points. So 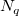 and
and 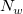 can be considered to be the average numbers of data points lying within distance
can be considered to be the average numbers of data points lying within distance 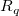 and
and  respectively for each node.
respectively for each node.
References
[1]. Franke R and Nielson G. smooth Interpolation of Large Sets of Scattered Data. Internat. J.Num. Methods Engrg. 1980, 15, pp:1691-1704.
[2]. Renka, R. J., Multivariate Interpolation of Large Sets of Scattered Data. ACM Transactions on Mathematical Software, Vol. 14, No. 2, June 1988, pp:139-148.
Related X-Functions
xyz_regular, xyz_renka, xyz_renka_nag, xyz_shep, xyz_sparse, xyz_tps
Keywords:worksheet
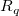 and
and  , to the grid nodes are considered. To make it easier for setting, two integers,
, to the grid nodes are considered. To make it easier for setting, two integers, 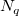 and
and 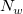 are used to calculate
are used to calculate 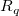 and
and  (parameters q and w of the function, and called Quadratic Interplant Locality Factor and Weight Function Locality Factor, respectively). Increase the value of
(parameters q and w of the function, and called Quadratic Interplant Locality Factor and Weight Function Locality Factor, respectively). Increase the value of 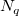 and
and 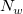 will make the calculation more global, vice versa. Generally speaking, setting
will make the calculation more global, vice versa. Generally speaking, setting 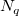 ≈
≈ 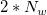 works fine and by default, Nq=18, Nw=9. However, the following constraints: 0<
works fine and by default, Nq=18, Nw=9. However, the following constraints: 0< 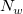 ≤
≤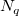 should be satisfied.
should be satisfied.
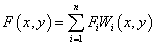
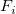 is the underlying function at nodes (
is the underlying function at nodes (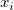 ,
, 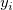 ), and
), and 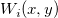 is the weights. To make the function more local,
is the weights. To make the function more local, 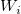 are calculated only by the data points lying in the circle with center (
are calculated only by the data points lying in the circle with center (
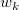 is:
is:
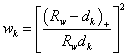
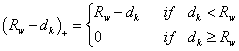
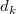 is the Euclidean distance between (x, y) and (
is the Euclidean distance between (x, y) and (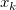 ,
, 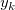 ):
):
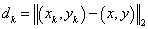
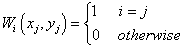
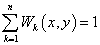
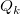 :
: