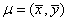follows bivariate normal distribution, we can study the relationship of the two variables by this test. The confidence ellipse is centered at 
, and the major semiaxis 
and major semiaxis 
are given by the following equations:
Create a scatter matrix plot as embedded graphs in worksheet
Please refer to the page for additional option switches when accessing the x-function from script
| Display Name |
Variable Name |
I/O and Type |
Default Value |
Description |
|---|---|---|---|---|
| Input | irng |
Input Range |
|
Specify the input data range. |
| Confidence Ellipse | ellipse |
Input int |
|
Specify whether to add confidence ellipse for each graph based on the chosen confidence level. |
| Confidence Level in % | conflevel |
Input double |
|
This is only available when the ellipse variable is set to 1. Use it to specify the confidence level in percentage for the confidence ellipses. This value must be greater than 0 and less than 100 |
| Linear Fit | fit |
Input int |
|
Specify whether to perform a linear fit to each pair of variables. When this is checked, the fitted line and the adjusted R^2 value will be added to each scatter graph. |
| Exclude Missing Values Listwise | missing |
Input int |
|
Specify whether to exclude missing values listwisely. That is, exclude the entire row for all datasets if there are any missing values in this row. |
| Output Results | rd |
Output ReportData |
|
This determines where the calculated data for the ellipse and the fit are stored. The default location is a new worksheet within the source workbook. |
| Result Graph | rt |
Output ReportTree |
|
This determines where the graphs will be stored. The default location is a new worksheet based on the GRAPH.OTW template within the source workbook. |
This X-Function can be used to create a scatter matrix of multiple variables with normal distributions, which can be used to determine if pairs of such variables correlate or not.
Confidence ellipse can be added to each scatter plot. This helps you to judge the correlation of the pair of variables plotted in the graph.
Linear fit can be performed to each scatter plot. The inclination angle of the fitted line indicates the direction of the correlation. If it is positive, this means that the increase of one variable is likely to cause the increase of the other variable. While a negative angle indicates a reverse relationship. The slope of the fit varies from -1 (perfectly negative correlation) to +1 (perfect positive correlation).
// Create a Scatter Matrix using columns 2, 3 and 5 of the specified Worksheet newbook na:=PlotMatrixEX op:=1; wo -a 3; // Add 3 columns col(1)=data(1,30); col(2)=uniform(30); col(3)=normal(30); col(4)=uniform(30); col(5)=col(3); plotmatrix irng:=[PlotMatrixEX]Sheet1!(2,3,5) ellipse:=1 conflevel:=50 fit:=1; // Here we create a new book with sheets for our data and our graphs. // We then use this same book for gathering Scatter Matrix results // for columns 1 and 2 in all sheets in our source book. newbook na:=PMEx2 op:=1; repeat 3 newsheet; loop(ii,1,4) { page.active = ii; // for each sheet col(1) = uniform(25); col(2) = uniform(25); } for( ii = 1 ; ii <= 4 ; ii++) { range rData = [PMEx2]$(ii)!(1,2); plotmatrix irng:=rData ellipse:=1 conflevel:=50 fit:=1 rd:=[STATS]MyScatterData rt:=[STATS]MyScatterGraphs; }
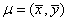Assuming the pair of two variables follows bivariate normal distribution, we can study the relationship of the two variables by this test. The confidence ellipse is centered at , and the major semiaxis and major semiaxis are given by the following equations:
where 
and are the variances of 
and 
, 
is the correlation coefficient of and .
For a given confidence level of 
, the constant 
is:
1) Confidence ellipse for the population mean:
2) Confidence ellipse for prediction:
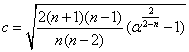
The inclination angle 
of the ellipse indicates the angle from the axis deasil. It is computed by the following equation:
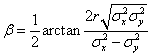
Keywords:confidence, ellipse, linear fit