2.10.1 plot_BA

1 Menu Information
2 Brief Information
3 Additional Information
4 Command Line Usage
5 Variables
- 5.1 Details of Lines and Fills TreeNode
6 Description
7 Algorithm
- 7.1 True Value Varies
- 7.2 True Value is Constant
8 References

Menu Information

Bland-Altman

Brief Information

Create Bland-Altman plot

Additional Information

Minimum Origin Version Required: 2020b

Command Line Usage

1.plot_BA -r 1 irng:=[Book1]Sheet1!(C"RV",D"IC",A"Subj.") diff:=1 trplot.fillloa:=1 trplot.fillcil:=0;

Variables

Display Name	Variable Name	I/O and Type	Default Value	Description
Input	irng	Input Range	<active>	Specify data ranges of Method1, Method2, and Subject, in sequence. Subject column is optional. Option list: 1st Method Specify data column for the first method 2nd Method Specify data column for the second method Subject Specify data column for Subject. This option is specified if your data has repeated measures for each subject. Your data will be grouped into subjects according to the Subject column you choose here. Multiple groups of subjects are supported.
X Axis	xaxis	Input int	Mean	Specify the values used for X axis. Option list: mean:Mean m1:1st Method m2:2nd Method geo: Geometric Usually used when Y Axis is specified as ratios.
Y Axis	yaxis	Input int	1	Specify the values used for Y axis. Option list: diffp:Difference % Difference / Mean X 100% diff:Difference This is the value used when Subject column is specified. ratio:Ratio Usually used when X Axis is specified as geo.
SD Multiplier for LoA	sd	Input double	1.96	Specify the multiplier factor of Standard Deviation for Limits of Agreement method.
Confidence Level in %	conf	Input double	95	Specify the confidence level in percentage.
True Value is Constant	trueval	Input int	0	Checking this option to use One Way Anova to get mean square for the residual for two methods separately. Available only when Subject is specified.
Plot Each Subject as One Bubble	bubble	Input int	1	Available only when Subject is specified. Specify whether to plot each subject as one bubble. When it is selected, bubble size is mapped to number of replicates for each subject. Otherwise, each data point is plotted as one symbol, and its color and shape is mapped to Subject column.
Mean Difference (bias) Estimation	diff	Input int	Subject Difference	Available only when Subject is specified. When True Value is Constant is checked, Mean Difference Estimation uses subject differenct. Option list: sub:Subject Difference indv:Individual Row
Confidence Interval Estimation for LoA	interval	Input int	MOVER	Available only when Subject is specified. Option list: "mover:Mover delta:Delta Method
Lines and Fills	trplot	Input TreeNode	<unassigned>	Check to show the desired reference lines and color-filled area. See details in the next table.
Mean of Pairwise Means	mpm	Input int	0	Mean of all pair-wise means: 0=false, 1=true.
Bland-Altman Ratio	ratio	Input int	0	Calculated as 0.5*(upper LoA - lower LoA)/mpm: 0=false, 1=true.
Output Results	rd	Output ReportData	[<input>]<new>	Specify the range of output data for plotting.

Details of Lines and Fills TreeNode

This trplot tree specifies all supported reference lines and filled intervals.

Syntax: trplot.Treenode:=<value>

Example: trplot.fillloa:=1

Treenode	Label	Type	Default	Description
mean	Mean	int	1	Line of Mean value.
equality	Line of Equality (Difference=0)	int	1	Line of Equality (Difference=0).
	Limits of Agreement	int	1	Limits of Agreement
fillloa	Fill Between LoA	int	0	Fill interval area between LoA.
cim	CI of Mean	int	0	Lines of upper and lower limits of confidence interval of mean. The confidence level is specified in Confidence Level in %.
fillcim	Fill Between CI of Mean	int	1	Fill area between confidence interval of mean. The confidence level is specified by Confidence Level in %.
cil	CI of Limits of Agreement	int	0	Lines of limits of Agreement
fillcil	Fill Between CI of LoA	int	1	Fill area between confidence interval of limits of Agreement. The confidence level is specified by Confidence Interval Estimation for LoA.

Description

This X-Function is used to create the Bland-Altman plot. A Bland-Altman plot is a graphic display of difference between two methods. It is typically plotting the differences of two methods against their mean, with mean difference and 95% confidence intervals for comparison.

Also see menu deails here.

Algorithm

True Value Varies

It is assumed that the repeated differences for a single subject are independent in this case. One way ANOVA is used to calculate mean square of the residual (measurement error) for differences of two methers.

$NOO=\frac{(\sum m_i)^2-\sum m_i^2}{(n-1)\sum m_i}$

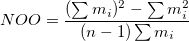
where 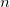$n$ is the number of subjects, 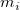$m_i$ is number of observations on subject i. If all the subjects have the same number of observations, m, this factor reduces to m.

$Average Difference Across Subjects = \frac{Mean Square of Model - Mean Square Of Error}{NOO}$

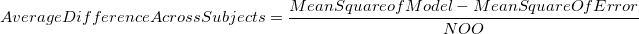
Total Variance for Single Differences on Different Subjects = Mean Square of Error + Average Difference across Subjects

Standard Deviation = Square Root of Total Variance for Single Differences on Different Subjects

Mean = mean of the individual differences

True Value is Constant

One Way Anova is used to get mean square for the residual (measurement error) for two methods separately.

$Multiplier = (1-\frac 1{n}\sum \frac 1{m})$

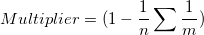
If the Multiplier of observations on each subjects are the same, the above formula can be simplified as:

$Multiplier = (1-\frac 1{m})$

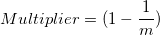
Standard Deviation = square root of (variance of differences between subject means + Multiplier of method1 * mean square of error of method1 + Multiplier of method2 * mean square of error of method2)