2.4.17 nlbeginr

1 Brief Information
2 Additional Information
3 Command Line Usage
4 X-Function Execution Options
5 Variables
6 Description
7 Examples
- 7.1 Example 1
- 7.2 Example 2
8 Related X-Functions

Brief Information

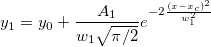
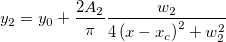
Start a nonlinear fitting session for multiple independent/dependent variables

Additional Information

Minimum Origin Version Required: 8.1 SR0

Command Line Usage

nlbeginr irng:=2 func:=gauss nltree:=tt option:=change_data;

X-Function Execution Options

Please refer to the page for additional option switches when accessing the x-function from script

Variables

Display Name	Variable Name	I/O and Type	Default Value	Description
Input	irng	Input Range		Specify the data to be fitted.
Fitting Function Name	func	Input string	<unassigned>	Specify the fitting function name.
NLFit Tree	nltree	Input/Output TreeNode	nlt	The tree that contains the information of fitting such as parameter values, standard error, etc. For more details, please refer to here.
Fitting Mode	mode	Input int	0	Specify the method to treat the input data for fitting. Option list: auto:Auto Origin automatically chooses a data mode. concat:Concatenate Fit All input datasets are concatenated and fitted as one curve. global:Global Fit All datasets are fitted globally. This mode should be used when you want to fit one model to multiple datasets with shared parameters. cons:Independent Fit - Consolidated Report All datasets are fitted independently. This mode should be used when you want to fit one model to multiple datasets without shared parameters and create the consolidated reports.
Dialog Theme	theme	Input string	<optional>	Specify a theme. The settings saved in it will be loaded to customize the fitting.
Notation of Parameters	pnotation	Input int	0	Specify the notation of parameters in the output tree. Option list: para:ParaName Use the parameter names as notation. abbr:Abbreviation Use the abbreviations of the parameters as notation. both:Both Use both names and abbreviations of the parameters as notation.
Parameter Initialization	init	Input int	0	Specify the status of parameter initialization. Option list: auto:Auto Origin automatically decides whether to enable parameter initialization according to the FDF file of the fitting function. enable:Enable Enable parameter initialization. disable:Disable Disable parameter initialization.
How to Initialize the NLFit Object	option	Input int	0	Specify how to initialize the NLFit Object. Option list: init_all:Init All Parameters Initialize all parameters and then do the fitting with these parameters. change_data:Only Change Data Keep the former settings and only change dataset, then do the fitting to the new dataset.

Description

This X-Function is used to start a nonlinear fitting session. Different from the nlbegin X-Function, whose input is XYRange, you can fit multiple independent/dependent variables function by nlbeginr. For example, the input can be XXYYYY, XYYY, XXXXY, etc.

Examples

Example 1

This example uses nlbeginr to fit with a built-in GaussianLorentz function, which is a combination of the Gaussian and Lorentz functions, input data is (x, y1, y2), sharing y0 and xc:

$y_1 =y_0+\frac {A_1}{w_1\sqrt{\pi /2}}e^{-2\frac{(x-x_c)^2}{w_1^2}}$

$y_2=y_0+\frac{2A_2}\pi \frac {w_2} {4\left( x-x_c\right) ^2+w_2^2}$

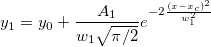
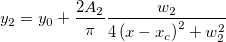
newbook;
string fname$ = system.path.program$ + "Samples\Curve Fitting\Lorentzian.dat";
impasc;
// Specify the input range, which follows 
// the independent/dependent order in FDF
nlbeginr (1,3,4) GaussianLorentz tt;
// Perform fitting
nlfit;
// Output results
tt.y0=;
tt.xc=;
tt.A1=;
tt.A2=;
tt.w1=;
tt.w2=;
// End the fitting session
nlend;

Fitted parameters are shown as follows:

Parameter	y0	xc	A1	A2	w1	w2
Value	-2.18829	25.01942	141.39931	95.83519	10.02691	1.92878

You can also see this tutorial.

Example 2

This example uses nlbeginr to fit with a built-in HillBurk function, which is a combination of the Hill and Burk functions, input data is (x1, x2, v1, v2):

$v_1 =Vm_1 \frac {x_1}{ K_{m1} + x_1 }$

$v_2=\frac{1}{V_{m2}}+\frac{ K_{m2} }{V_{m2}} x_2$

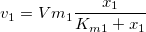
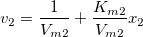
newbook;
string fname$ = system.path.program$ + "Samples\Curve Fitting\Enzyme2.dat";
impasc;

wks.col3.type=4;

// Specify the input range, which follows 
// the independent/dependent order in FDF (x1, x2, v1, v2)
nlbeginr (1,3,2,4) HillBurk tt;
// Perform fitting
nlfit;
// Output results
tt.Vm1=;
tt.Km1=;
tt.Vm2=;
tt.Km2=;
// End the fitting session
nlend;