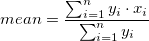 where
where 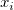 and
and  is the X and Y values of the ith data point in the input dataset.
is the X and Y values of the ith data point in the input dataset.
Minimum Origin Version Required: 8.0 SR6
diststats iy:=col(3) percent:=col(4) quantile:=col(5);
Please refer to the page for additional option switches when accessing the x-function from script
| Display Name |
Variable Name |
I/O and Type |
Default Value |
Description |
|---|---|---|---|---|
| Input | iy |
Input XYRange |
|
Specify the input data. |
| Percent of Integral Area | percent |
Input vector |
|
This variable is related to quantile. Assign a vector to this variable. Then for each value k in the vector, the kth percentile will be output. |
| Peak Direction | dir |
Input int |
|
This X-Function assumes that there is a peak in the input data. It will locate it. The user is required to specify the direction of the peak.
Option list:
|
| Index of Peak | ipeak |
Output int |
|
Specify the output of the index of the data point which is the peak in the input data. |
| X Peak | xpeak |
Output double |
|
Specify the output of the X value of the data point which is the peak in the input data. |
| Y Peak | ypeak |
Output double |
|
Specify the output of the Y value of the data point which is the peak in the input data. |
| Mean | mean |
Output double |
|
Specify the output of the mean of the input dataset. See its computation in the Algorithm part. |
| Median | median |
Output double |
|
Specify the output of the mean of the input dataset. See its computation in the Algorithm part. |
| Quantile | quantile |
Output vector |
|
Specify the output of the quantiles correspond to the values in the vector that is assigned to the percent variable. |
This function can be used to execute distribution statistics on an XY range. The input data's X values should be monotonically increasing and the Y values should be greater than 0. Otherwise, the X-Function cannot be used.
fname$ = system.path.program$ + "Samples\Curve Fitting\Gaussian.dat"; newbook; impasc; dataset aa={0,0.01,25,50,99.99,100}; col(4)=aa; diststats iy:=col(2) percent:=aa quantile:=col(5);
Mean
The weighted arithmetic mean is calculated:
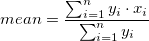 where
where 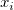 and
and  is the X and Y values of the ith data point in the input dataset.
is the X and Y values of the ith data point in the input dataset.
Median
First the sum of Y value of all data points is calculated:
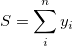
We suppose there is an M=0.5*S, for your data, the formula below is always coming into existence:
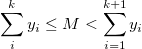
And the median we want is Median=X[K].
Quantile
Integration is performed on the whole input data to calculate the absolute area. Then for each value k in the vector assigned to the percent variable, the function finds a value m so that if one integrates the input curve from the first X value to m, the absolute area of this section will be of k percent of the total area.