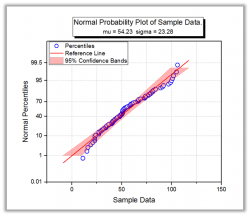
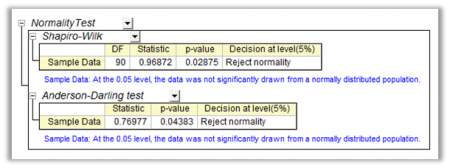
A normality test is used to determine whether sample data has been drawn from a normally distributed population (within some tolerance). A number of statistical tests, such as the Student's t-test and the one-way and two-way ANOVA require a normally distributed sample population. If the assumption of normality is not valid, the results of the tests will be unreliable.

|

|
Six different normality tests are available in Origin. Please look at the simple rule of selecting methods in table below.
For more details, please refer to the Choosing Normality Tests and Interpreting Results chapter
| Normality Test | Summary |
|---|---|
| Shapiro-Wilk | Common normality test, but does not work well with duplicated data or large sample sizes. |
| Kolmogorov-Smirnov | For testing Gaussian distributions with specific mean and variance. |
| Lilliefors | Kolmogorov-Smirnov test with corrected P. Best for symmetrical distributions with small sample sizes. |
| Anderson-Darling | Can give better results for some datasets than Kolmogorov-Smirnov. |
| D'Agostino's K-Squared | Based on transformations of sample kurtosis and skewness. Especially effective for “non-normal” values. |
| Chen-Shapiro | Extends Shapiro-Wilk test without loss of power. Supports limited sample size (10 ≤ n ≤ 2000). |
The missing values in the data range will be excluded in the analysis
From Origin 2015, missing values in the grouping range and the corresponding data values will be excluded in analysis. In the previous version, missing values in the grouping range will be considered as a group.
To perform a normality test from the menu
|
Topics covered in this section: |